前回開催させて頂きました7月早解き大会②(ヤジリン)の問題が難しく、解説が欲しいと要望がありましたのであくまでも自分の解き方ではありますが解説させて頂きます。

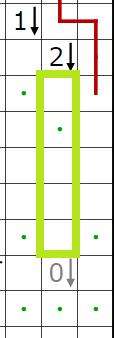
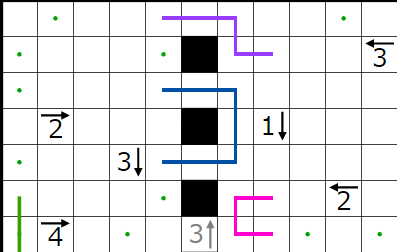
↑問題はこちら
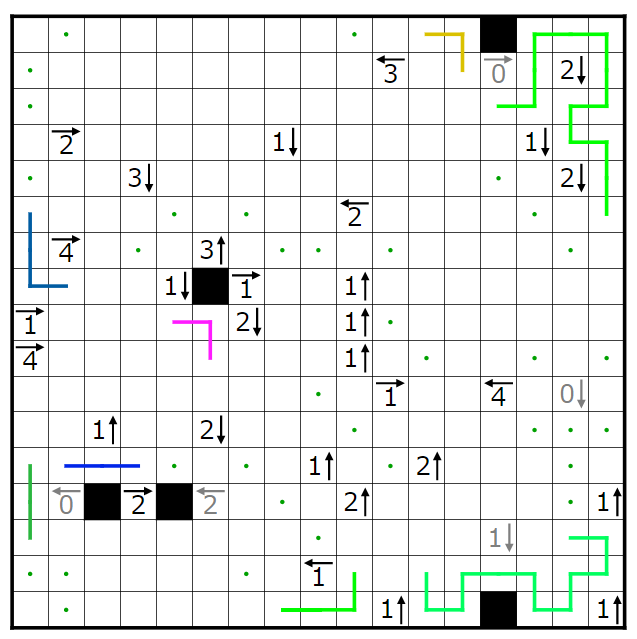
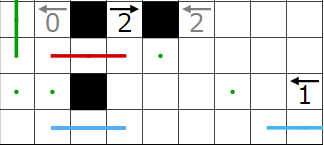
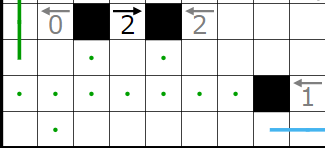
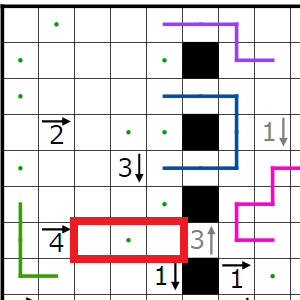
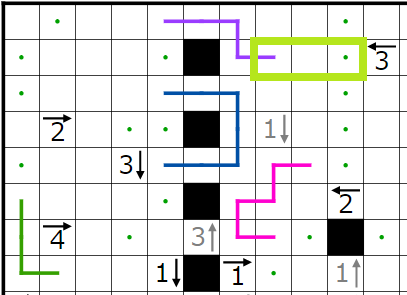
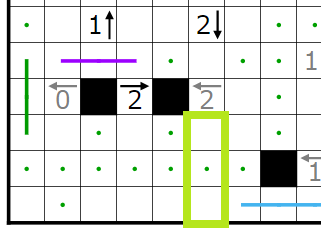
とりあえず単純仮定等々で決まるところまで埋めてみました。点・は黒マスが入らなく線が通るマスであることを表します。
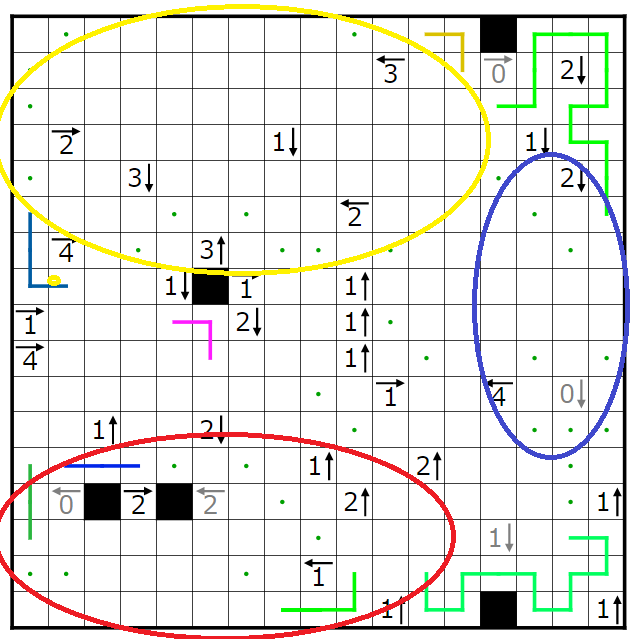
左下、右、左上の順に説明します。
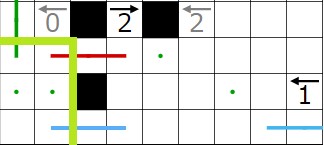
左下
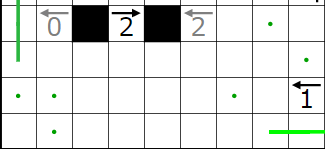
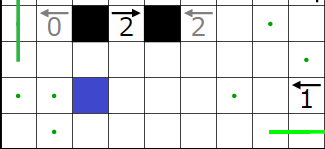
右


左上
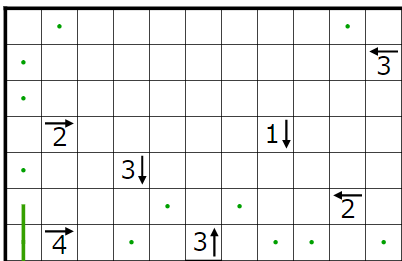
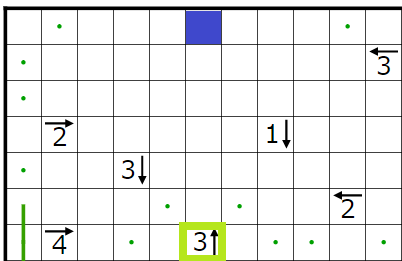
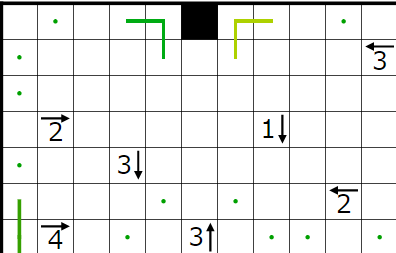
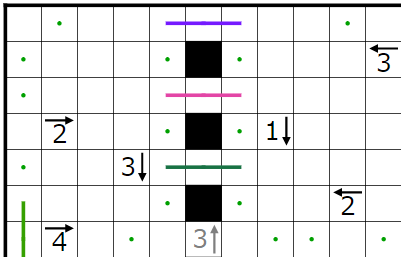
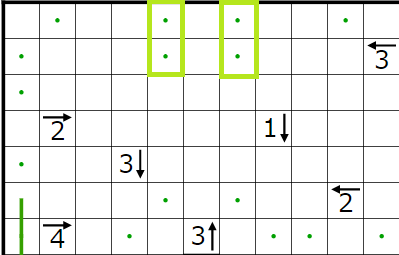

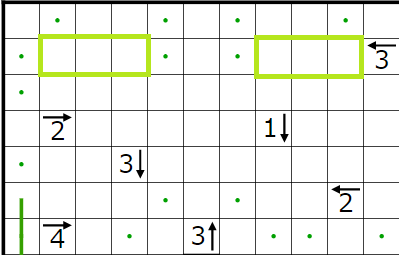

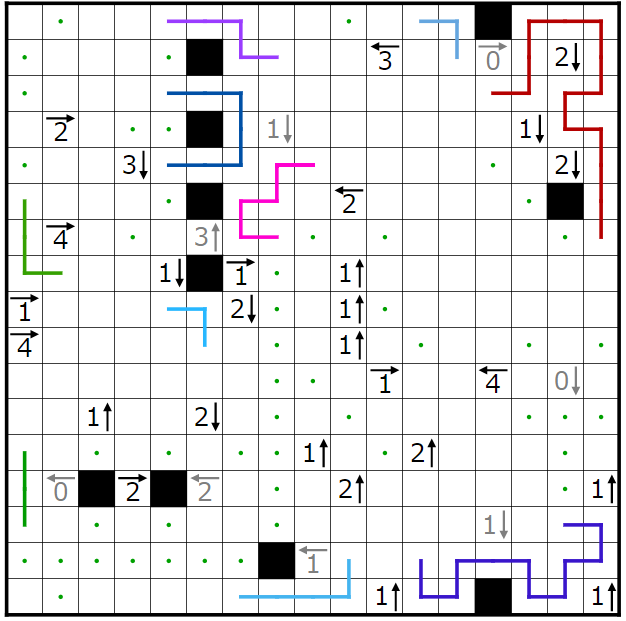
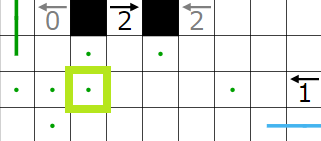
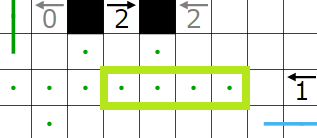
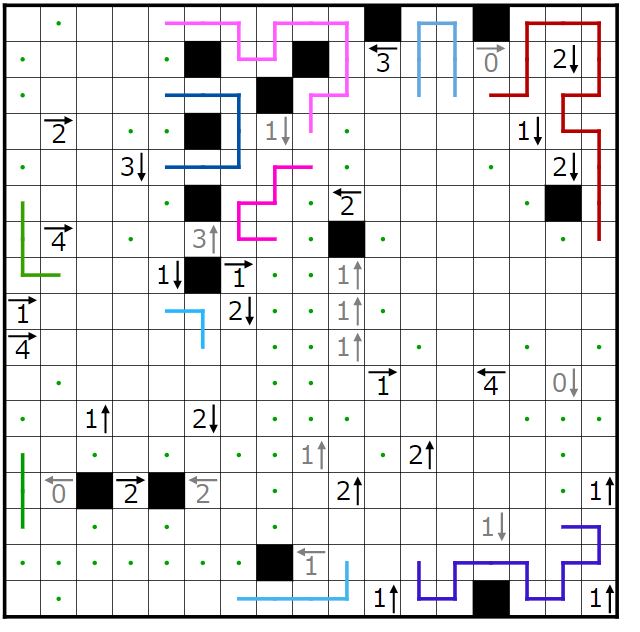
とりあえず今まで決まったところと、1↓のヒントによって決まる点・を打ったところです。
余談ですが、今回の問題は0のヒントでバーッと点・を最初に打たれるよりも1のヒントを使って、あるところが解き進んでから気づかないと点・が打てないようにしたら時間が稼げるんじゃないかなーと思ってそういう1を意識的に入れるようにしてみました。
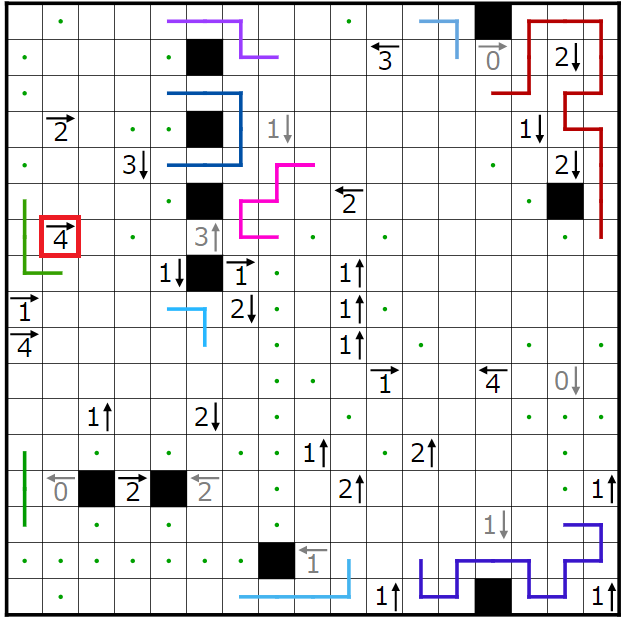
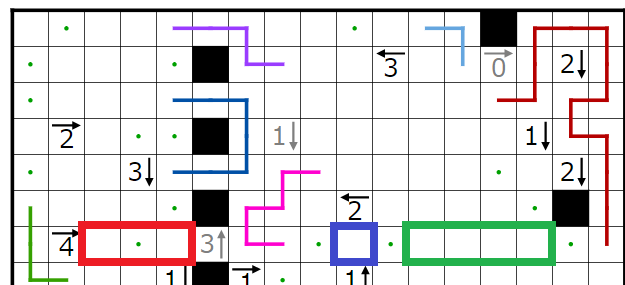
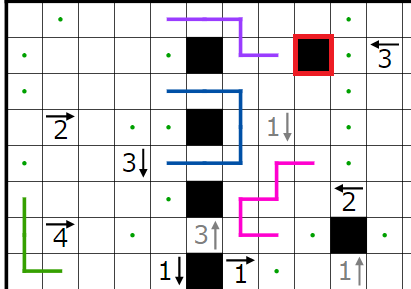
次に、赤四角で囲まれた4→について考えます。
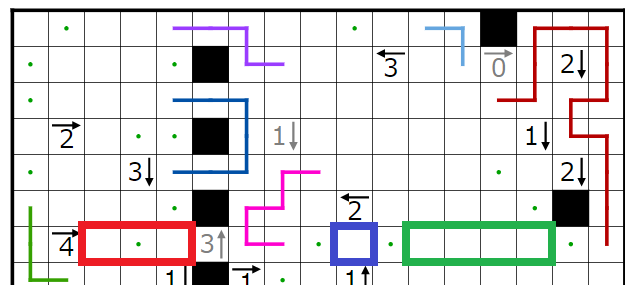
赤四角には黒ますが最大2個
青四角には黒マスが最大1個
緑四角には黒マスが最大2個
入ります。
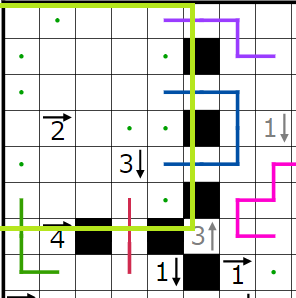
赤四角の部分には黒マスが1個、
青マスの部分には黒マスが1個、
緑マスの部分には黒ますが2個
最大入ることになります。4→のヒントより、それぞれの部分に最大の個数の黒マスを入れないといけないので、
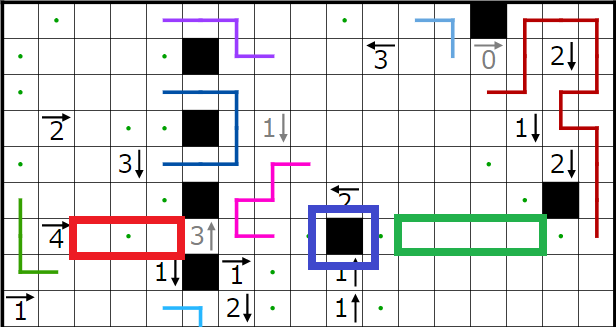
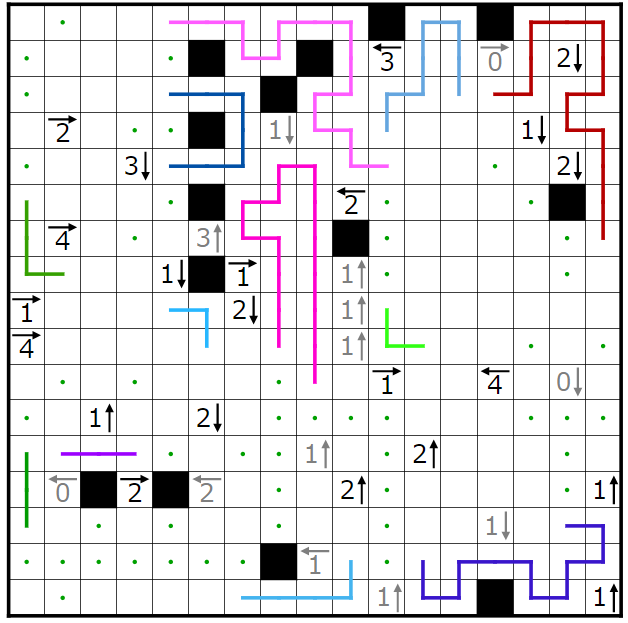
以上のことから決まるところと、1↑のヒントより確定するところを埋めた図です。
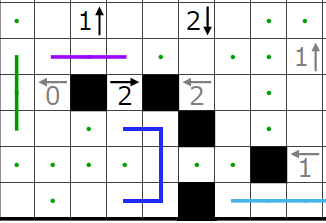
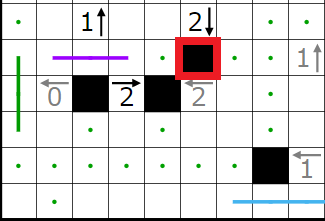
左下の2↓が一部決まるのを言い忘れていたので解説します。
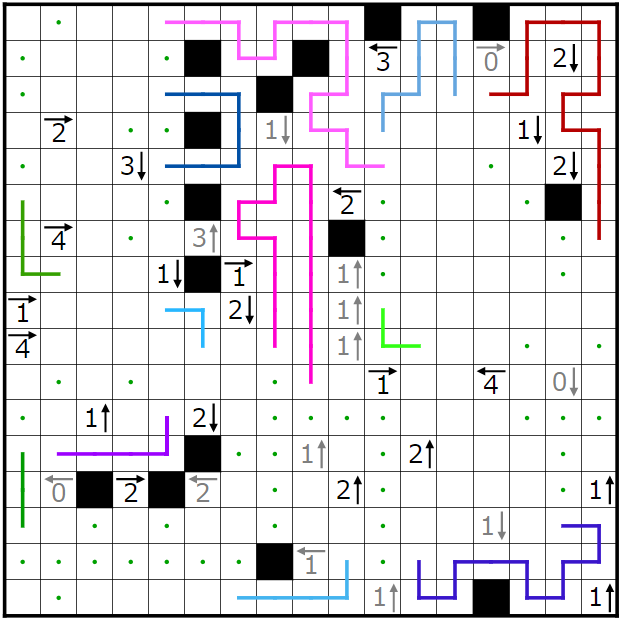
ここまで確定しました。
前編はここまでです。後編はまた後日書きます。