優勝 @pronter氏 08分52秒

第2位 @ek_bm氏 10分23秒

第3位 @homerestaurant3氏 15分57秒

第4位 @buyaketa氏 16分55秒

第5位 @ten986氏 17分31秒

第6位 @charmychachacha氏 20分31秒

第7位 @SP1_winter氏 20分47秒

第8位 @bara9598氏 22分05秒

第9位 @euextra氏 22分59秒

第10位 @WrdmntlstIT氏 24分15秒

第11位 @volxa氏 30分13秒

第12位 @scl_is_0氏 32分25秒

第13位 @rikkati氏 34分12秒

第14位 @sane_sanesuke氏 34分51秒

第15位 @nyamau氏 45分04秒

第16位 @heno_code氏 47分46秒

第17位 @pleiades_puz氏 49分23秒

第18位 @4DVector氏 57分43秒

以上になります！

優勝された焼きもうふ（@pronter）氏おめでとうございます！！！

皆様ご参加ありがとうございました！！！！！

閉会の言葉

ご参加いただいた皆様お疲れさまでした！！

今回の問題は、対称配置を決めてから比較的難しい決まり方をするように数字・方向を調整するように作ってみました！
　少し前ツイッターで出題した問題をそういう風に作ってみたところ、決まり方を作りながら発見することができて面白いかな…と思ったので大きい盤面でも同じようにしてみたというところなのですが、配置に意図が無いのでどこから解けば良いのか非常に分かりづらく茫洋とした問題になったかなあと思います。
　うーむ、しかし今回は難しすぎたか…難しいです。

・

次回大会は9月14日（土）の22時からの予定です！

それでは皆様ご参加ありがとうございました！！！

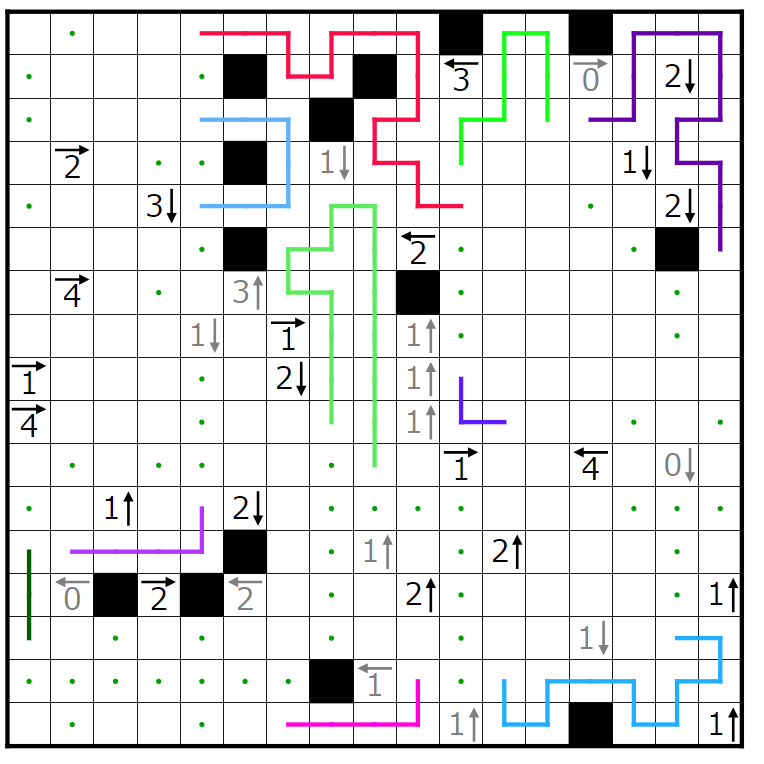
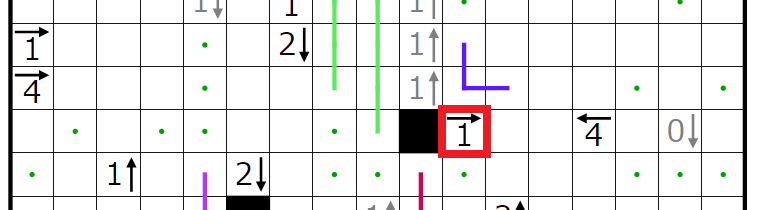
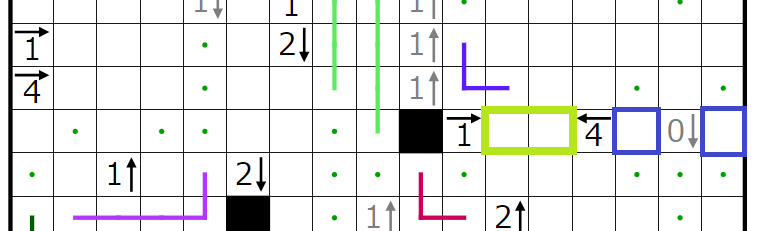
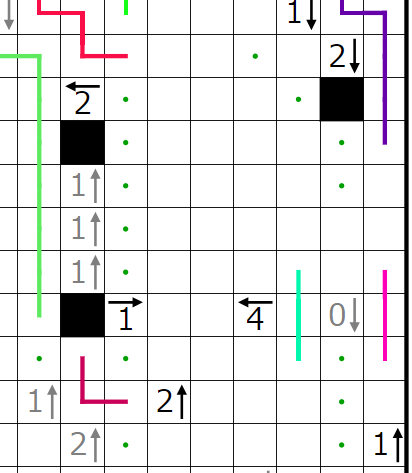
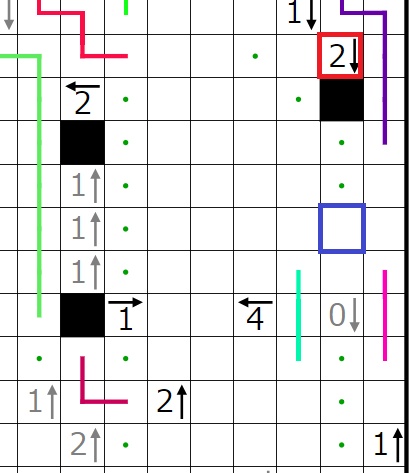
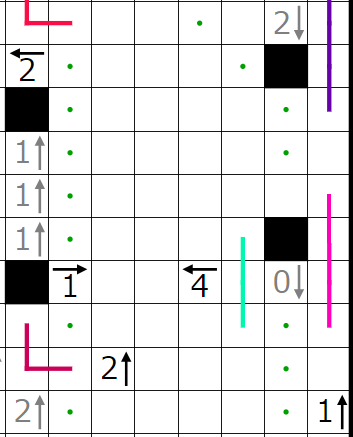
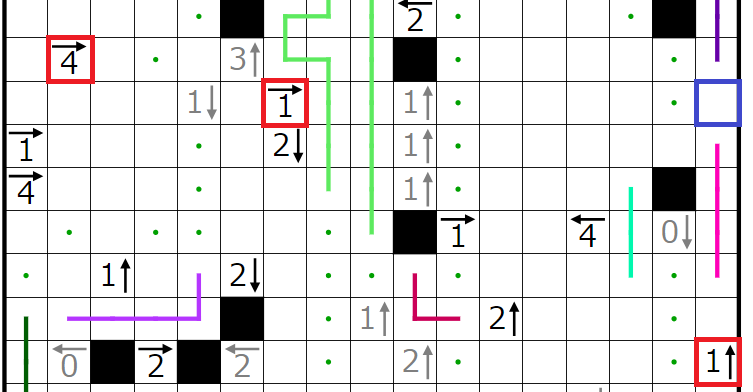
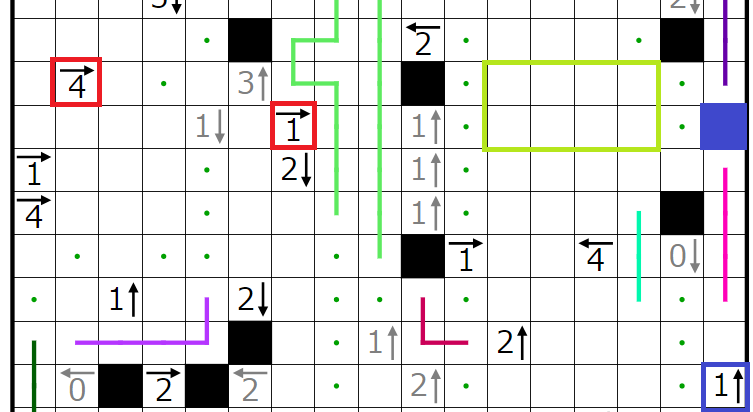
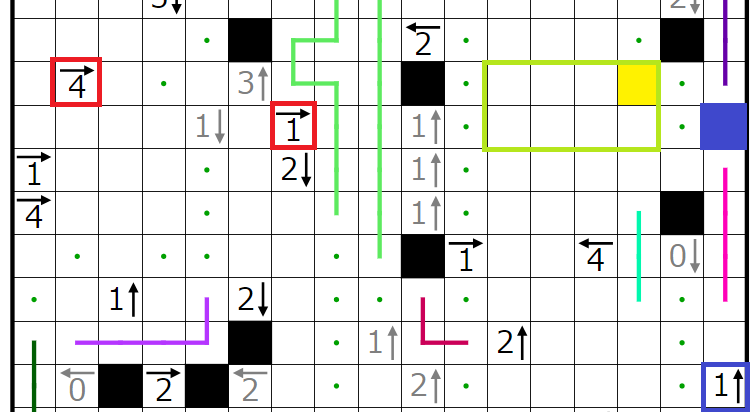
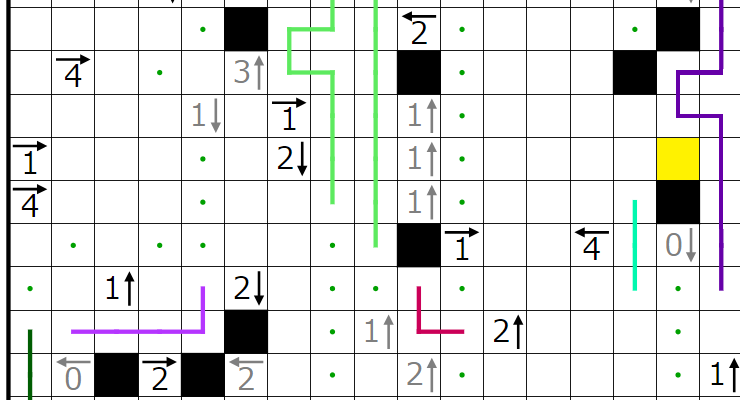
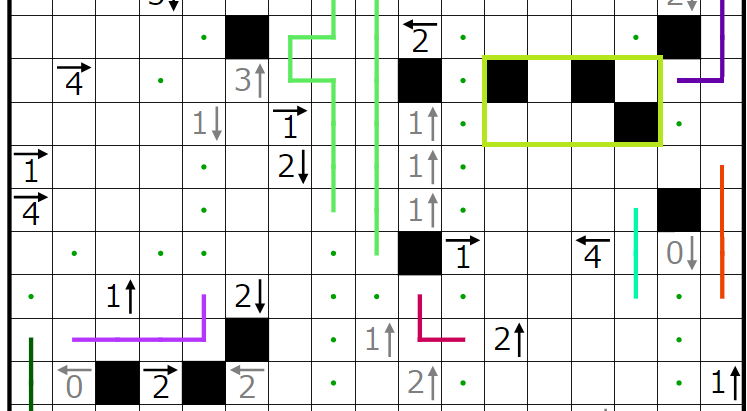
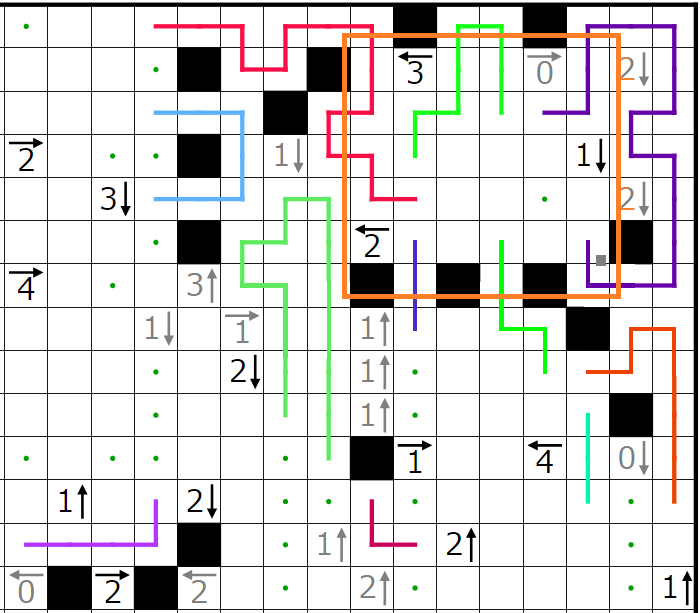
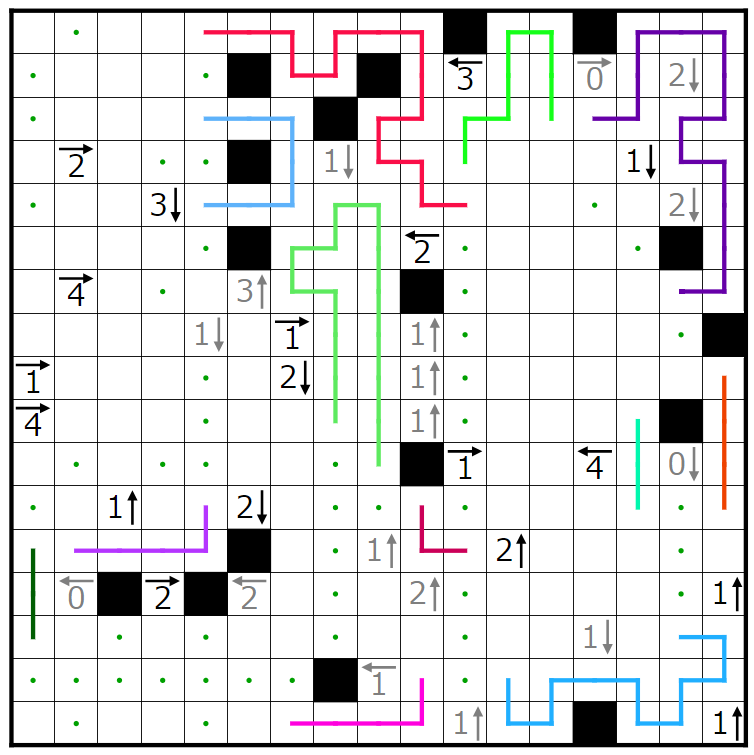
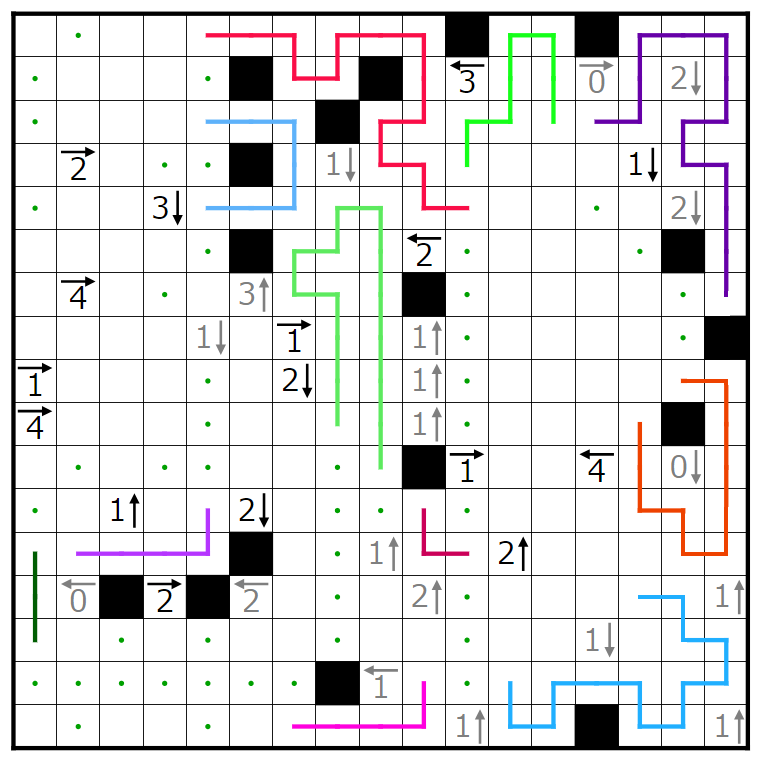
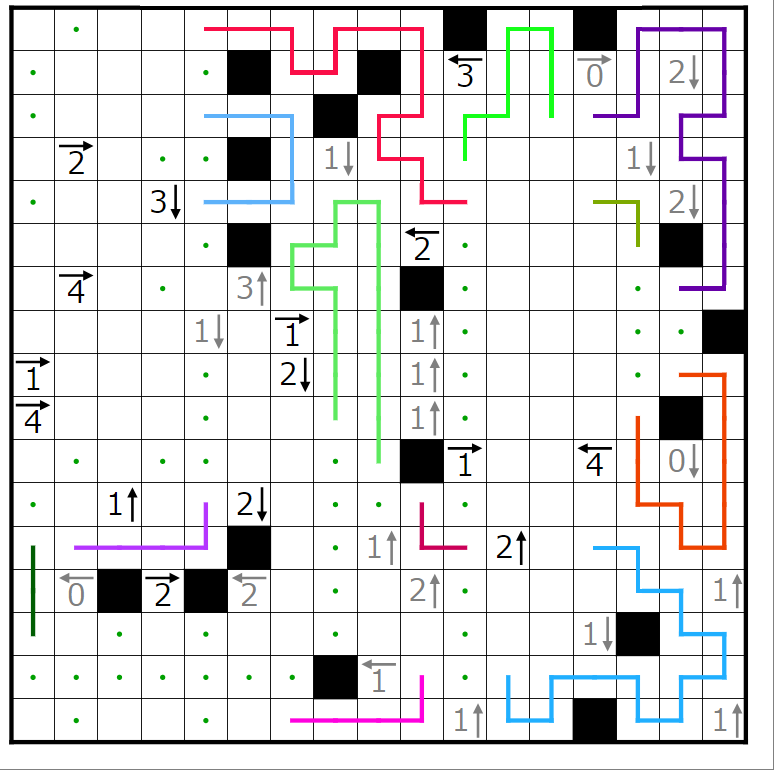
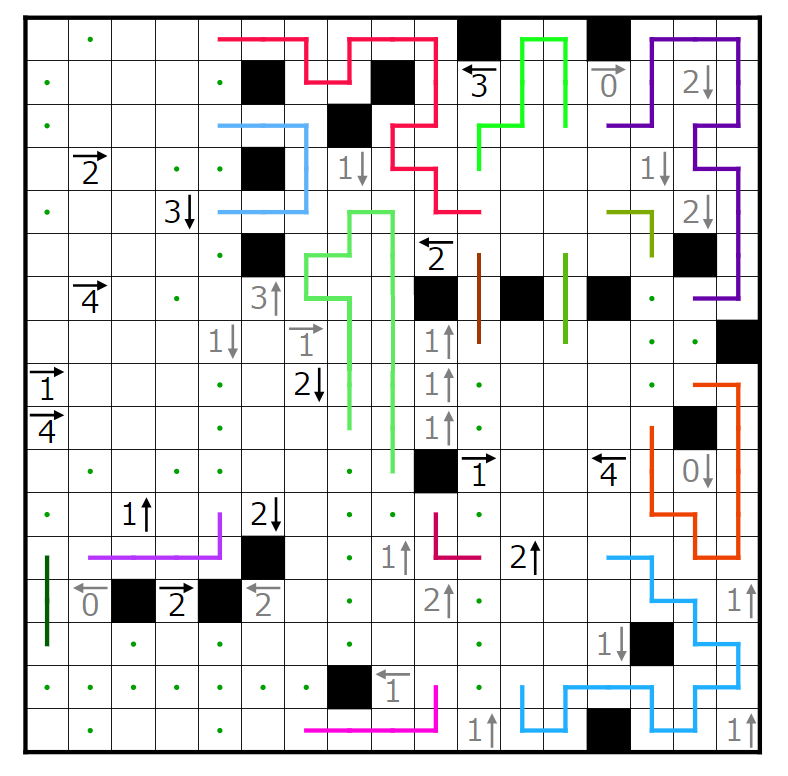
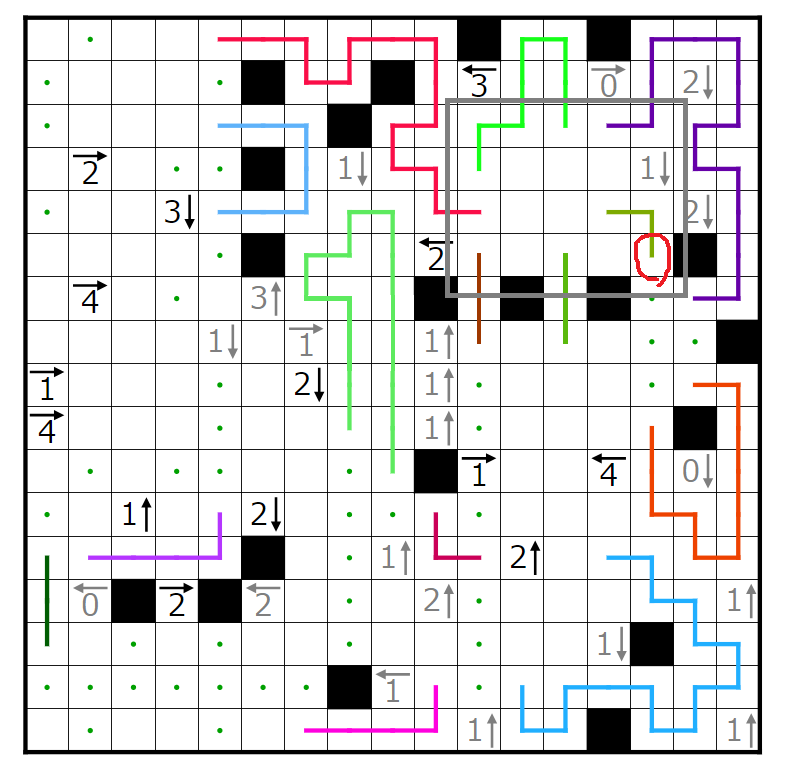
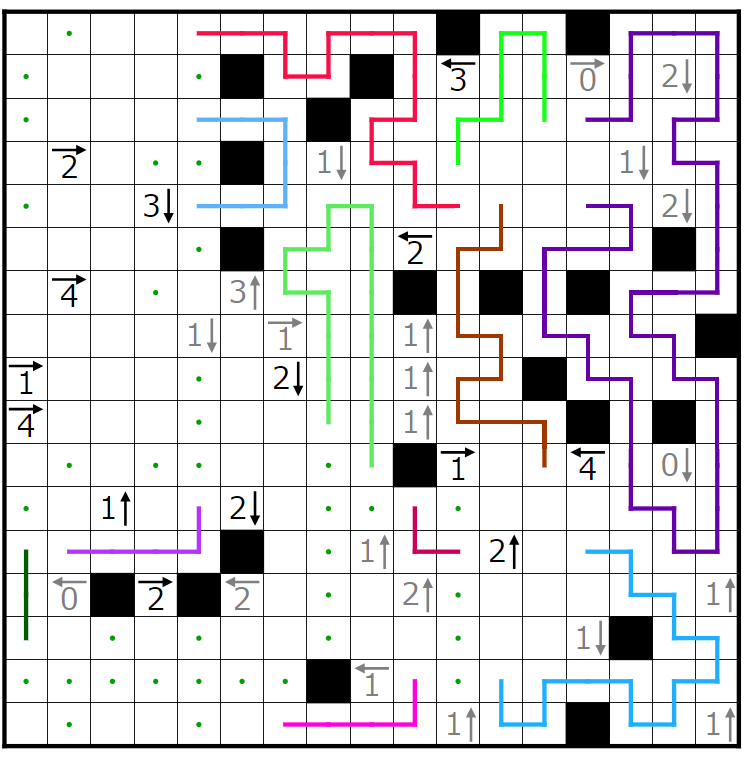
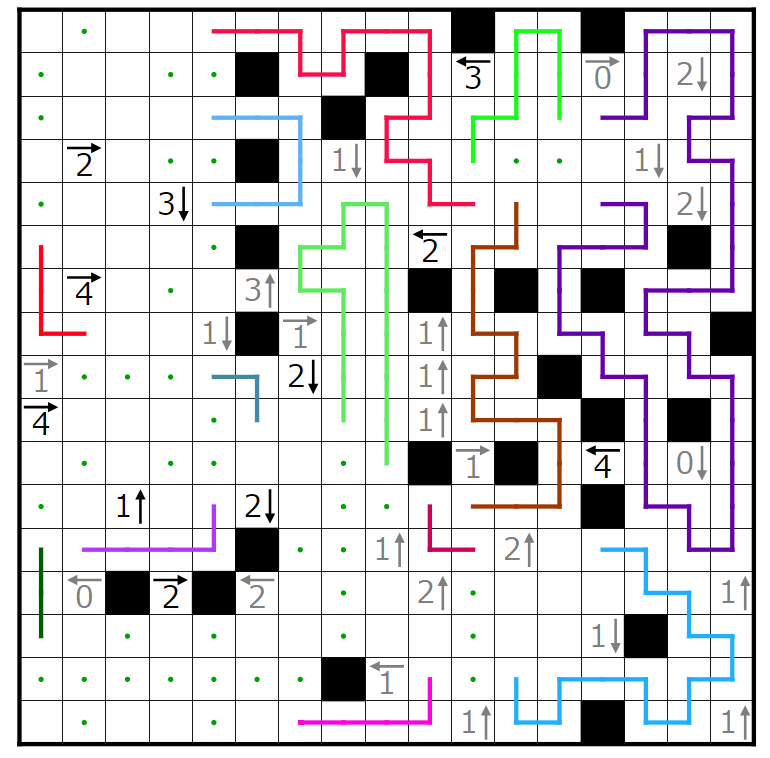
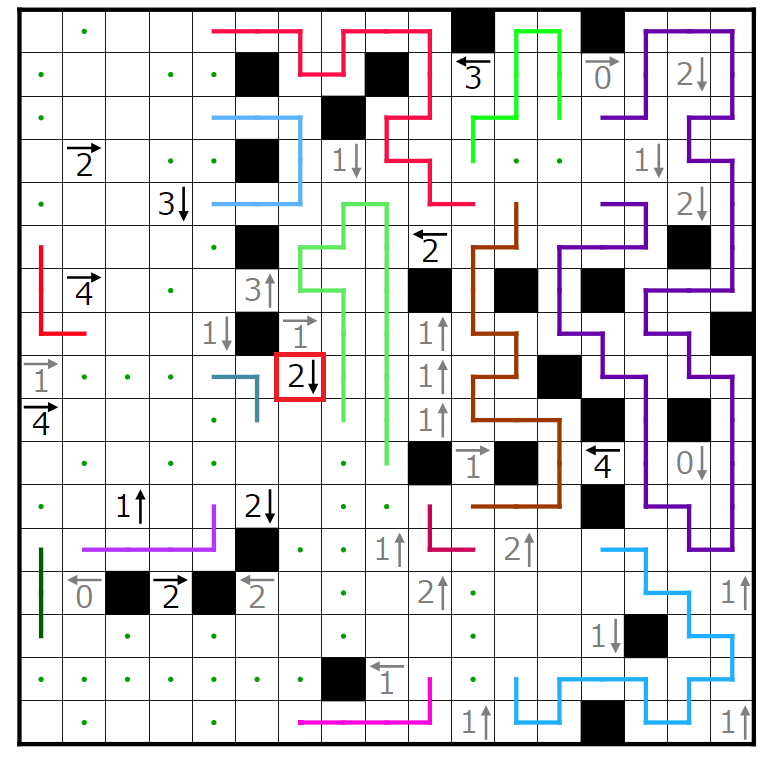
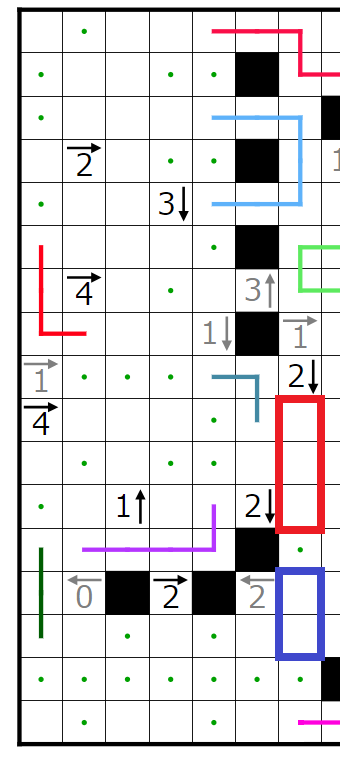
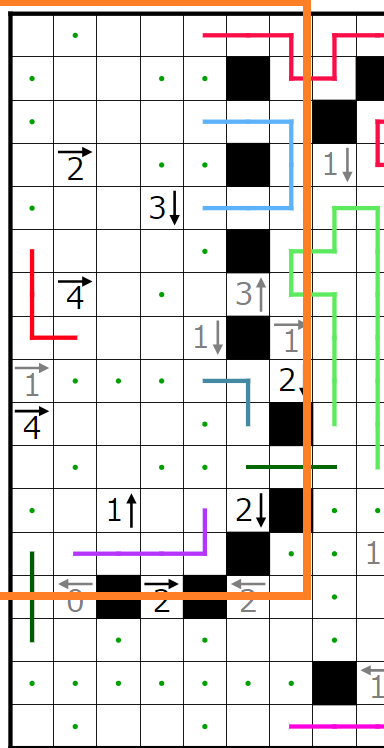
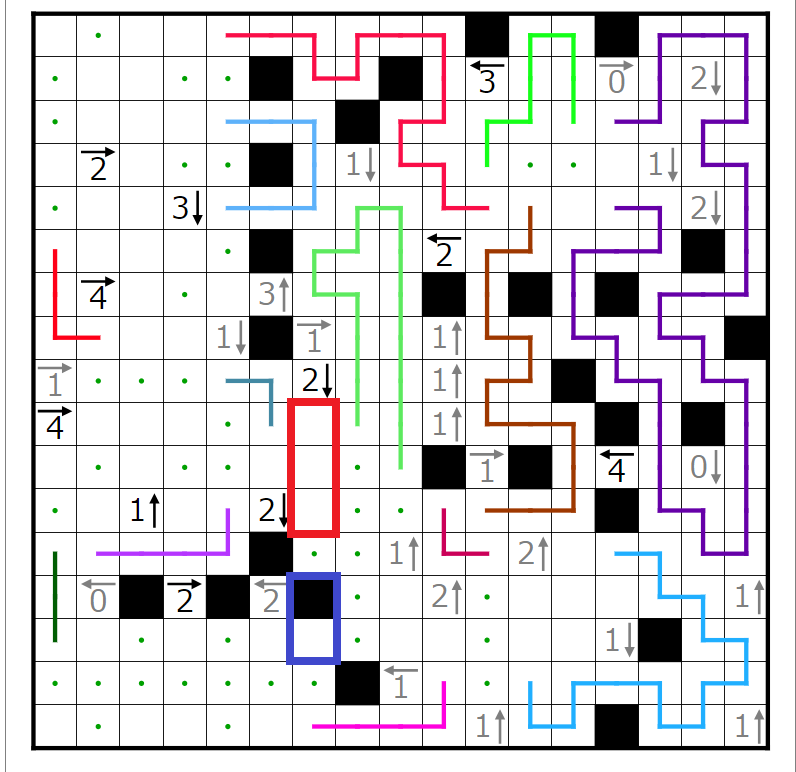
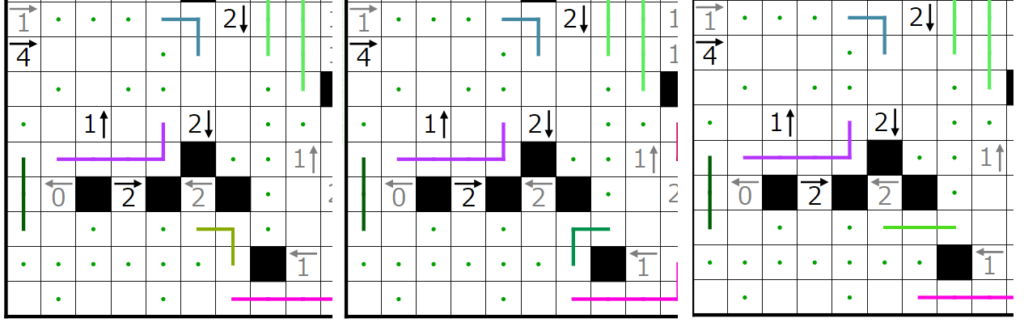
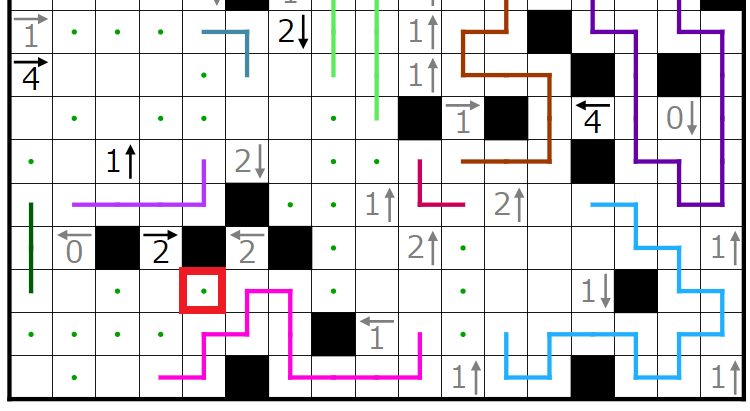
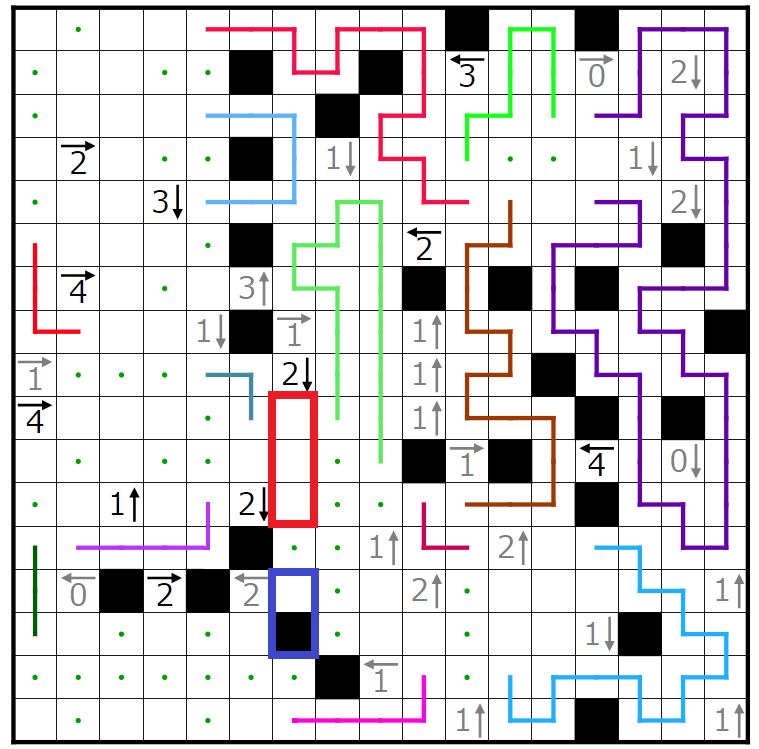
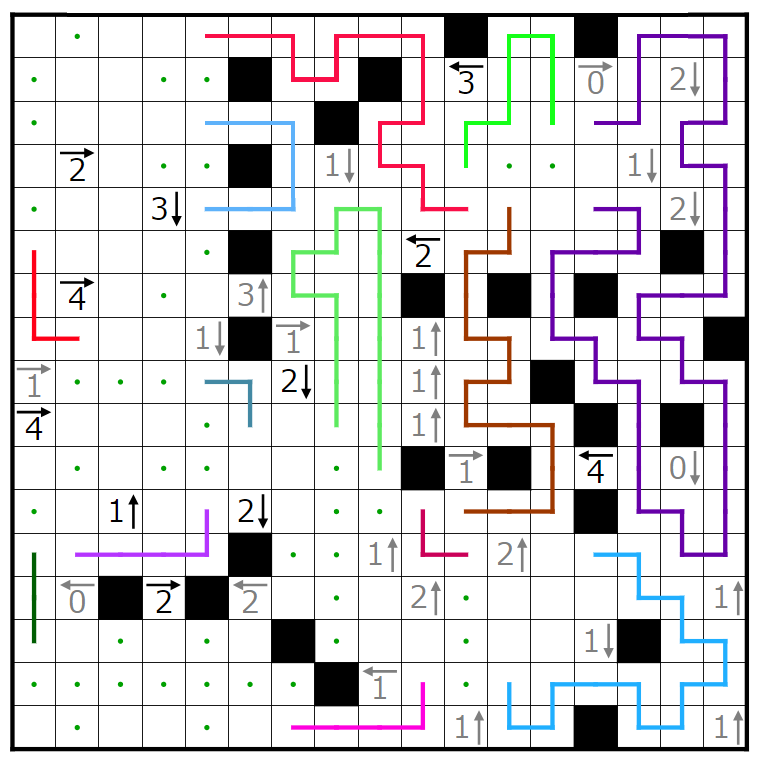
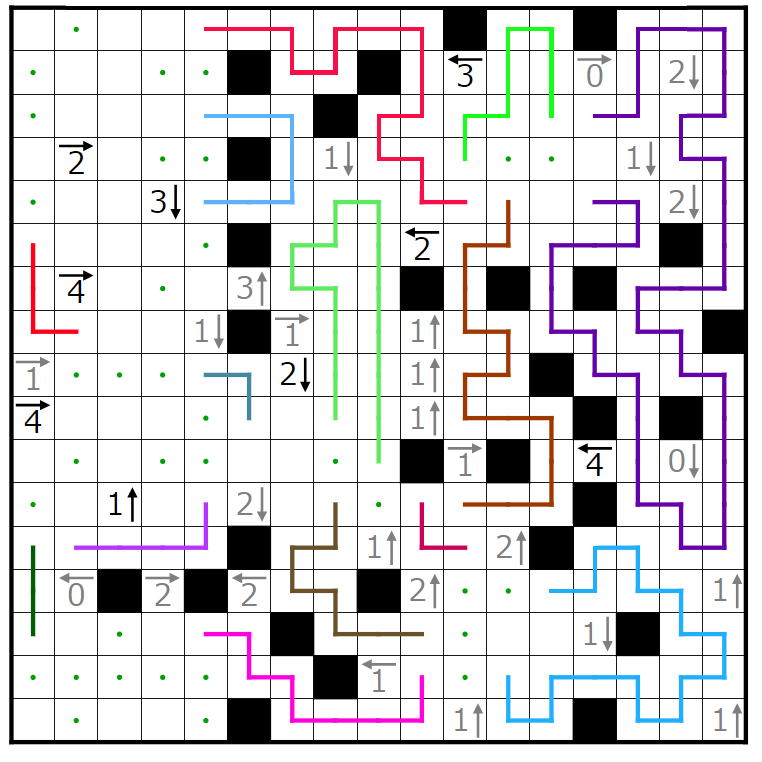
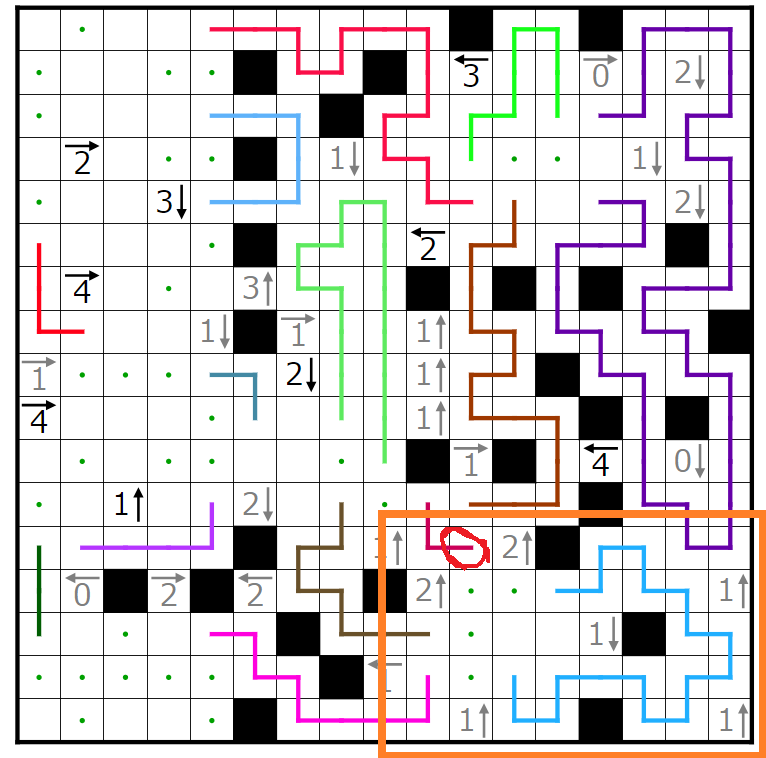
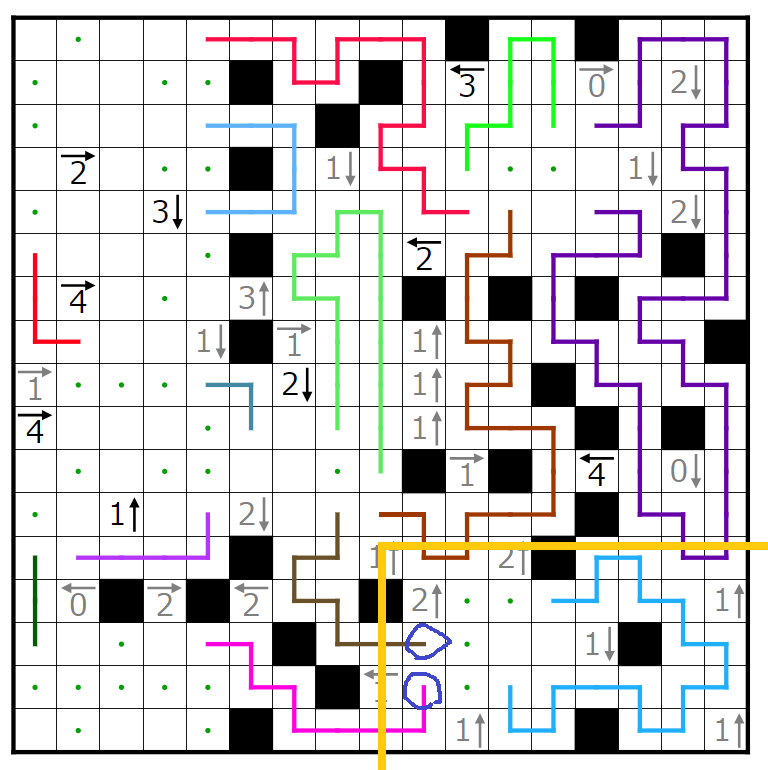
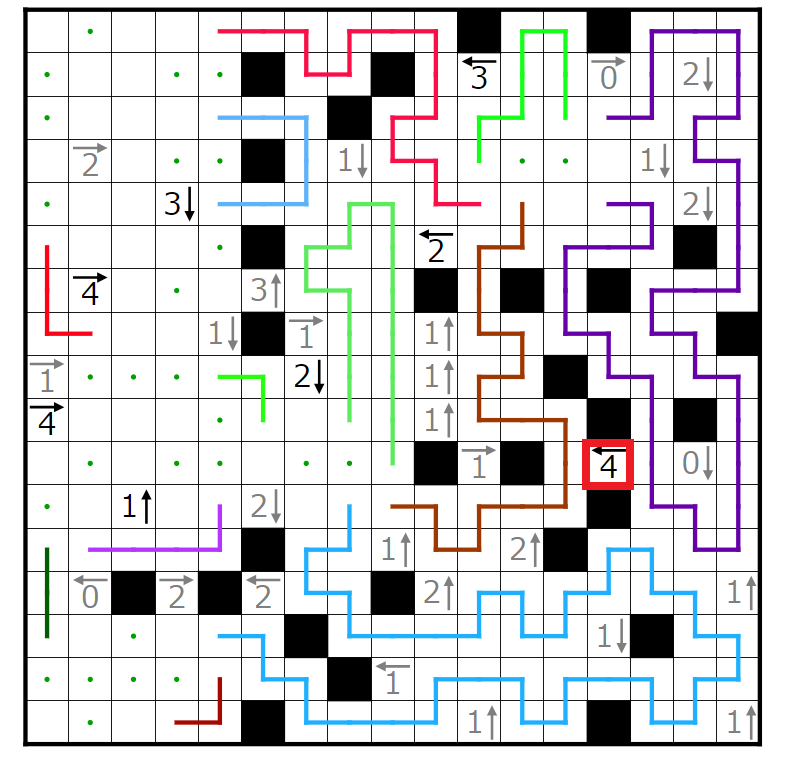
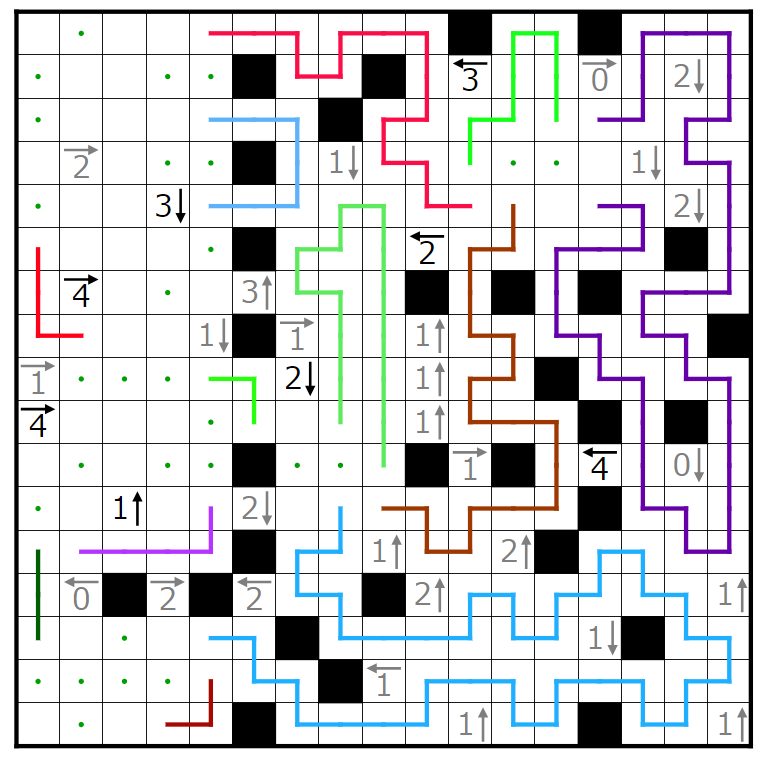
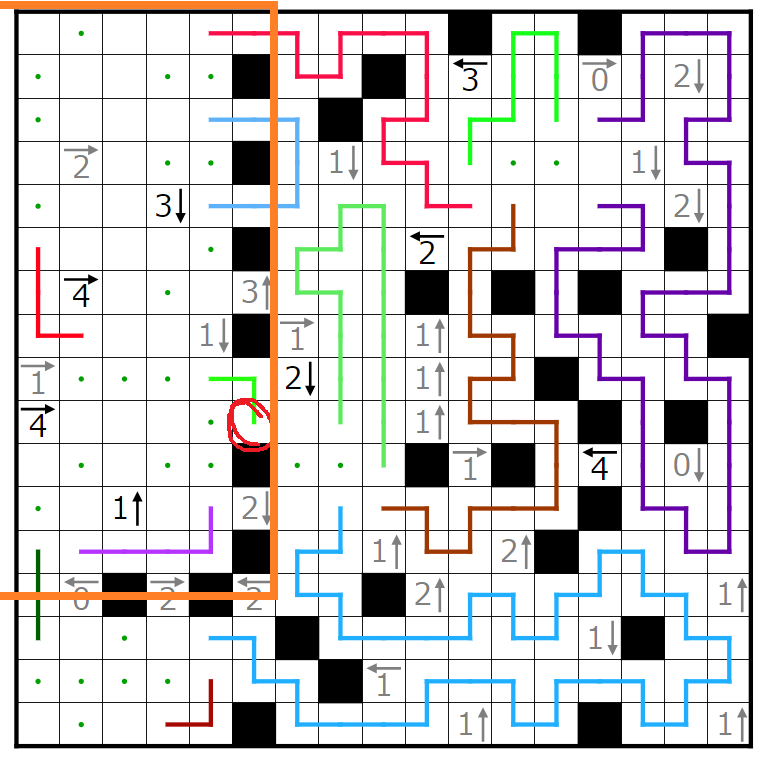
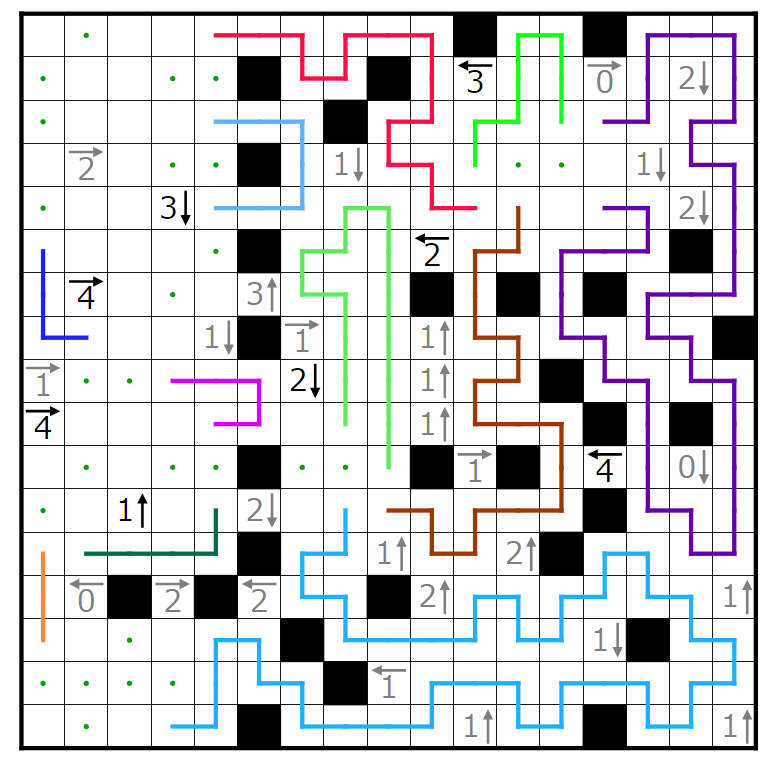
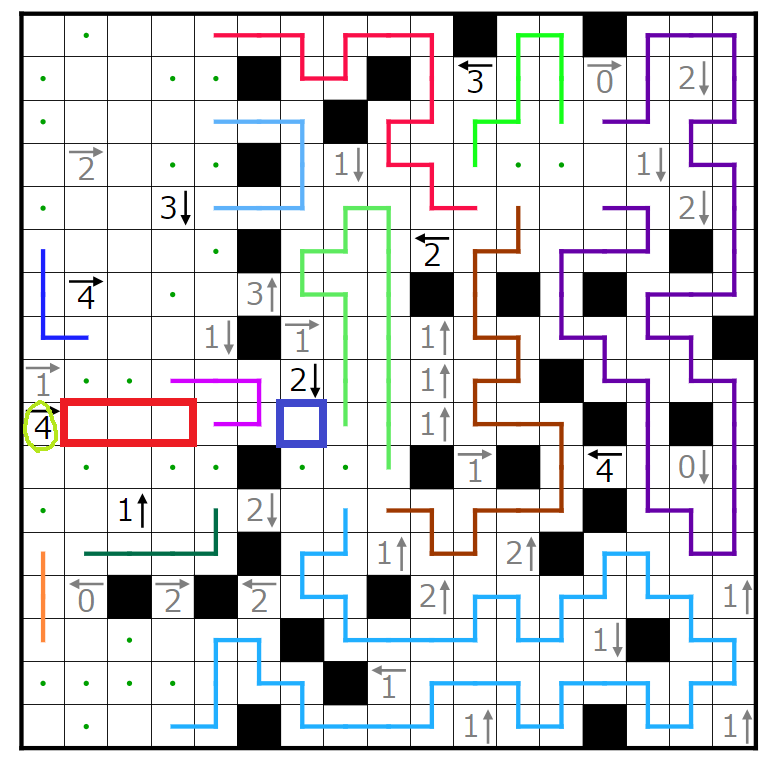
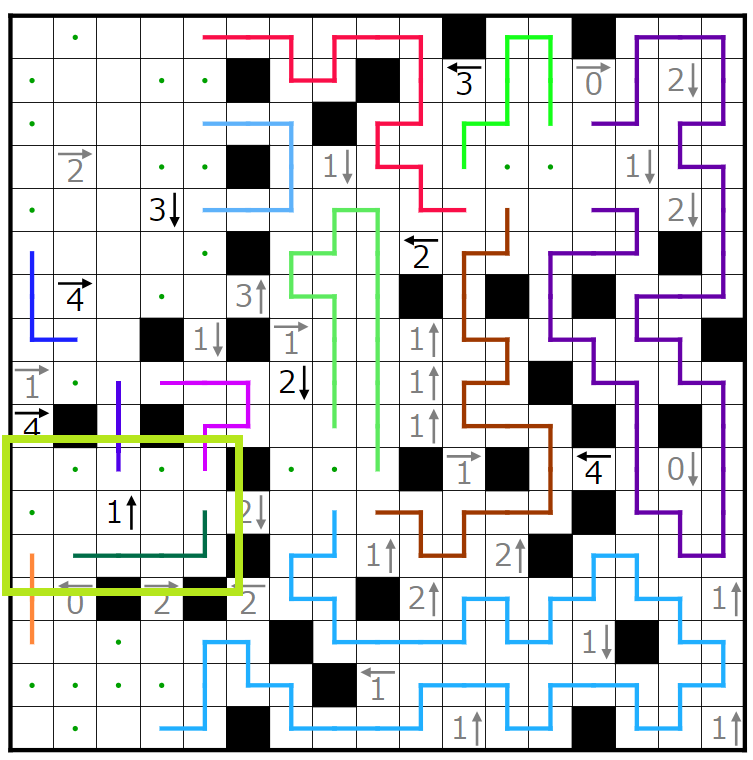
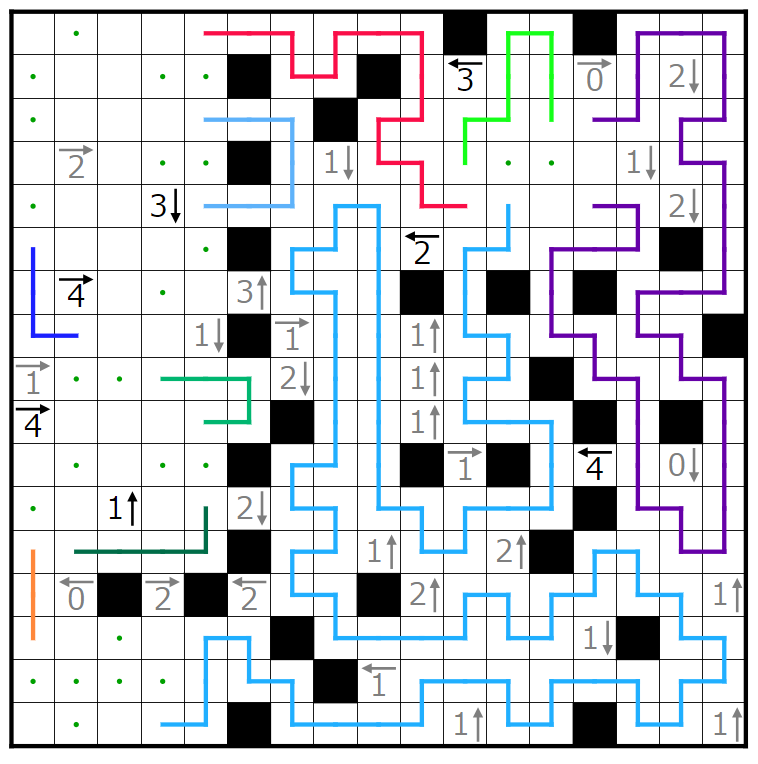
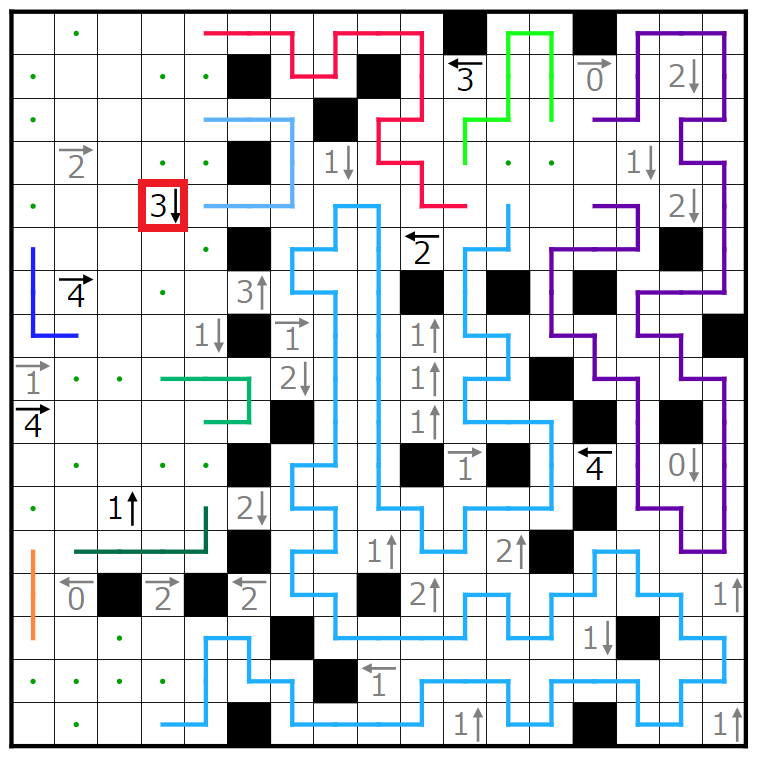
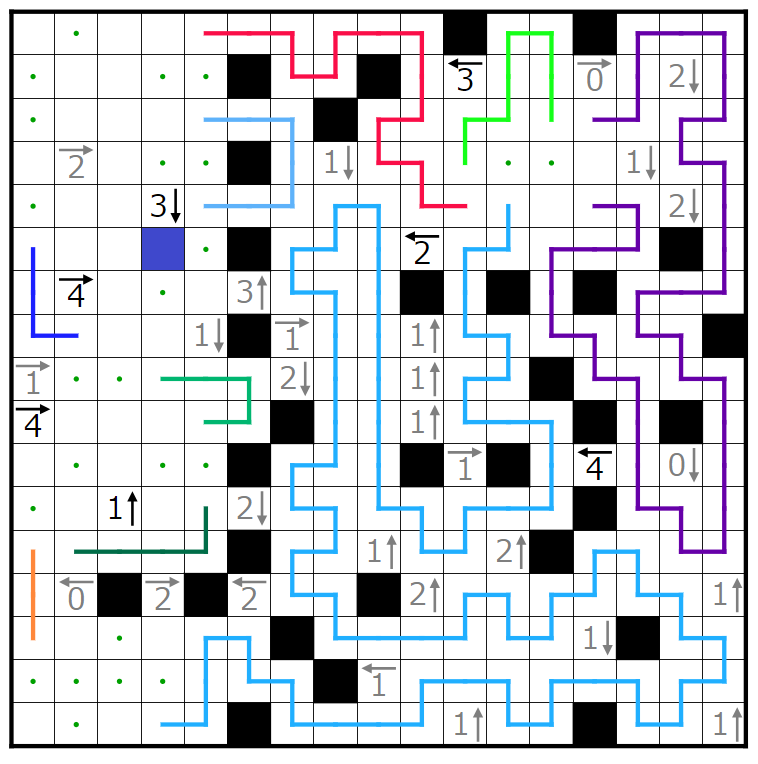
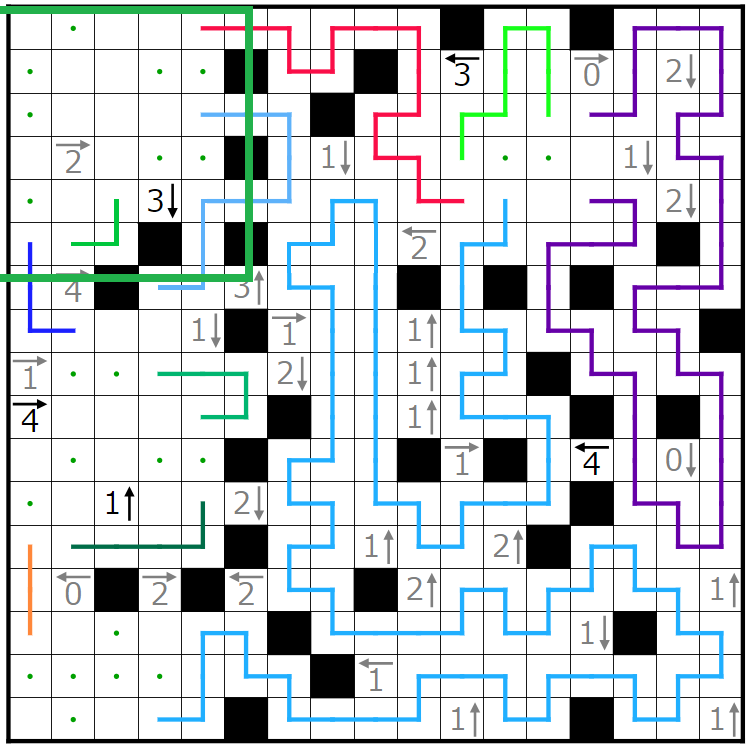
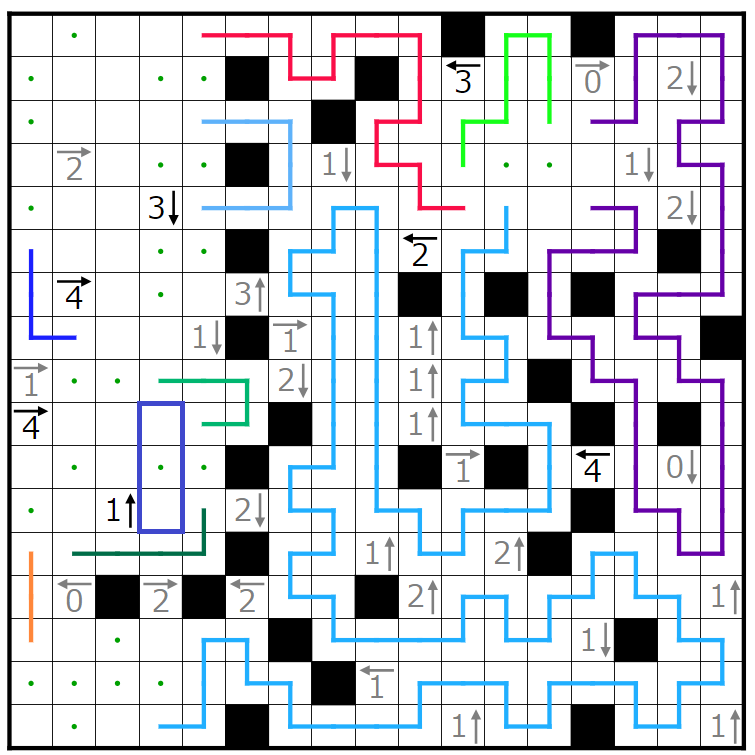
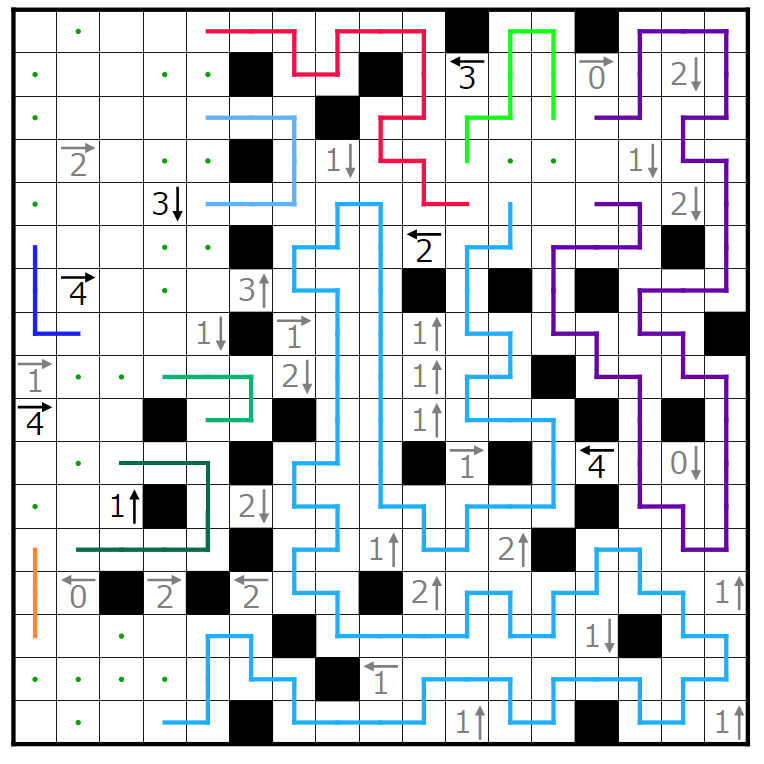
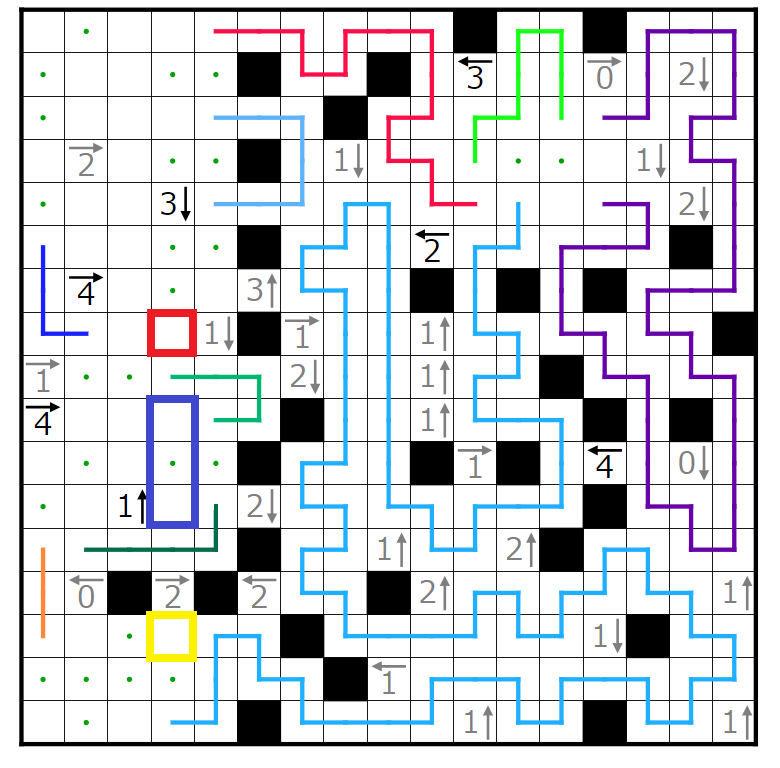
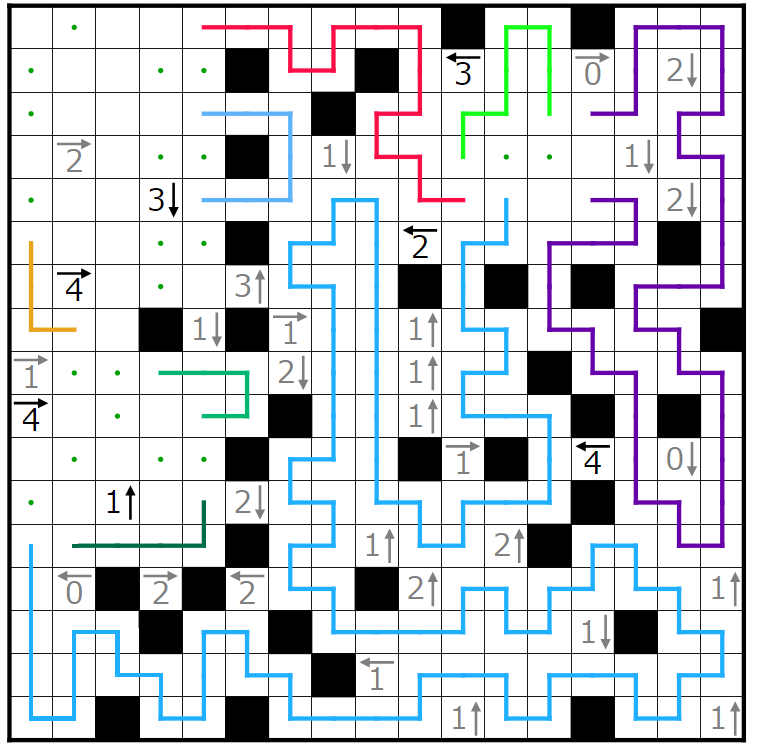
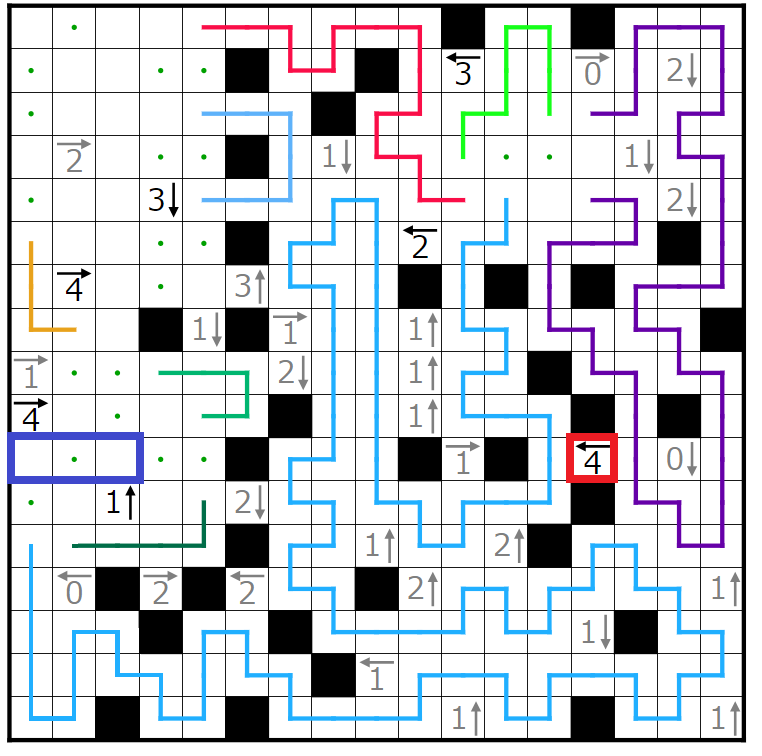
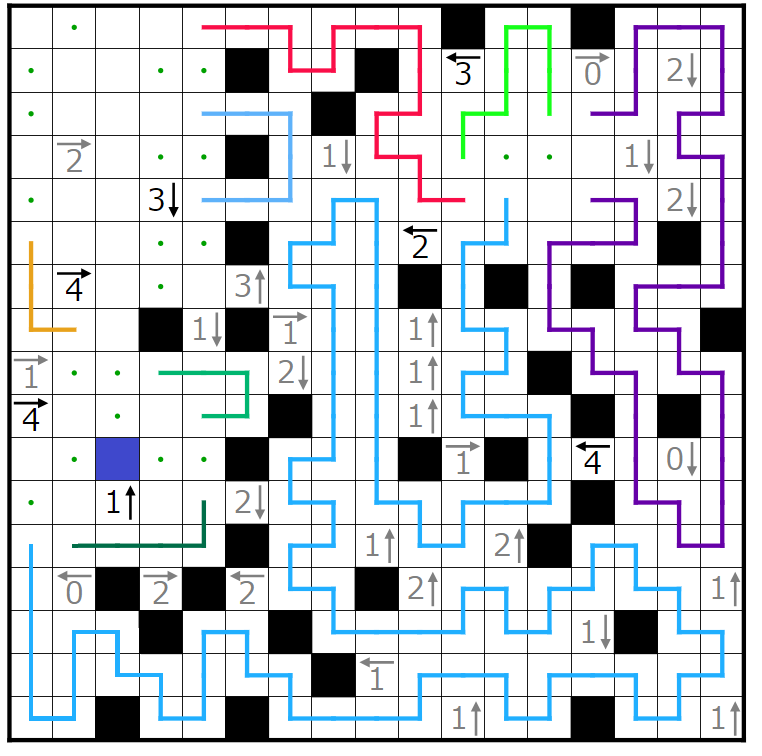
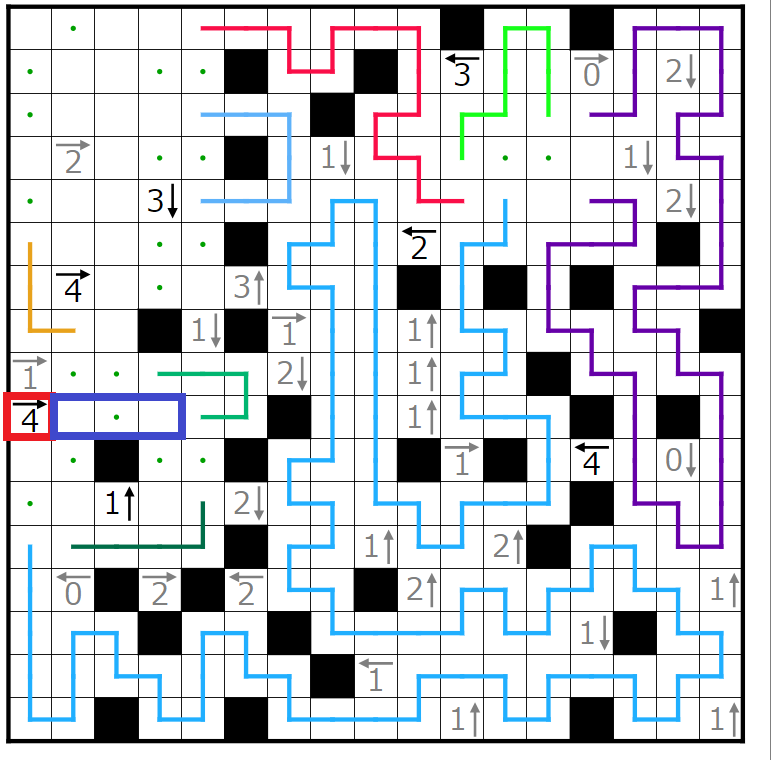
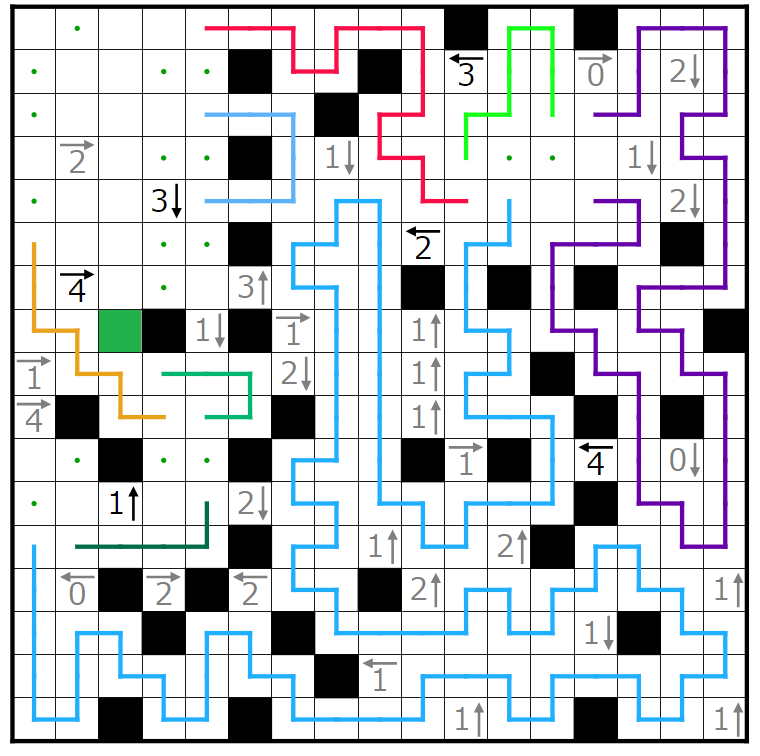
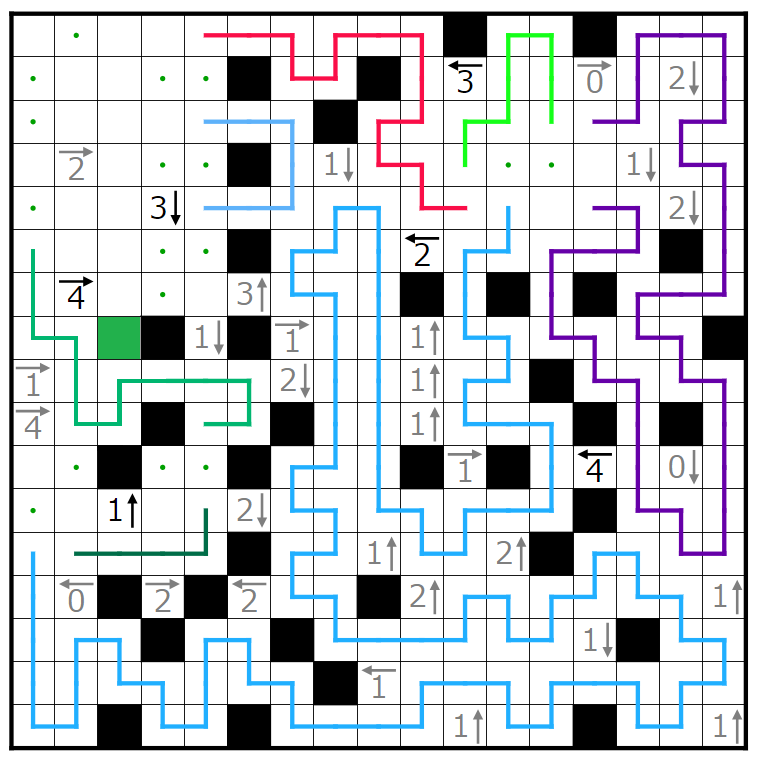
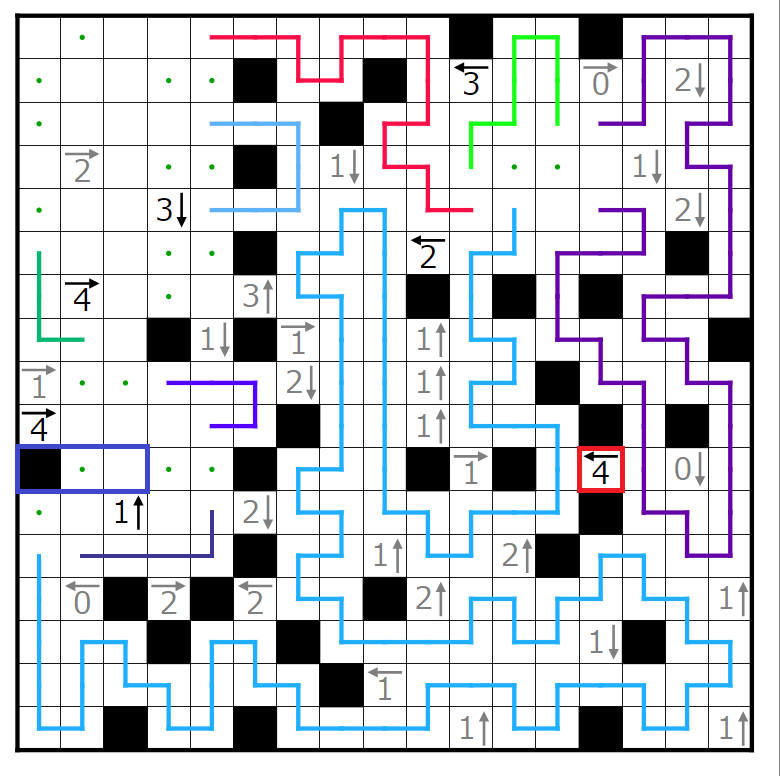
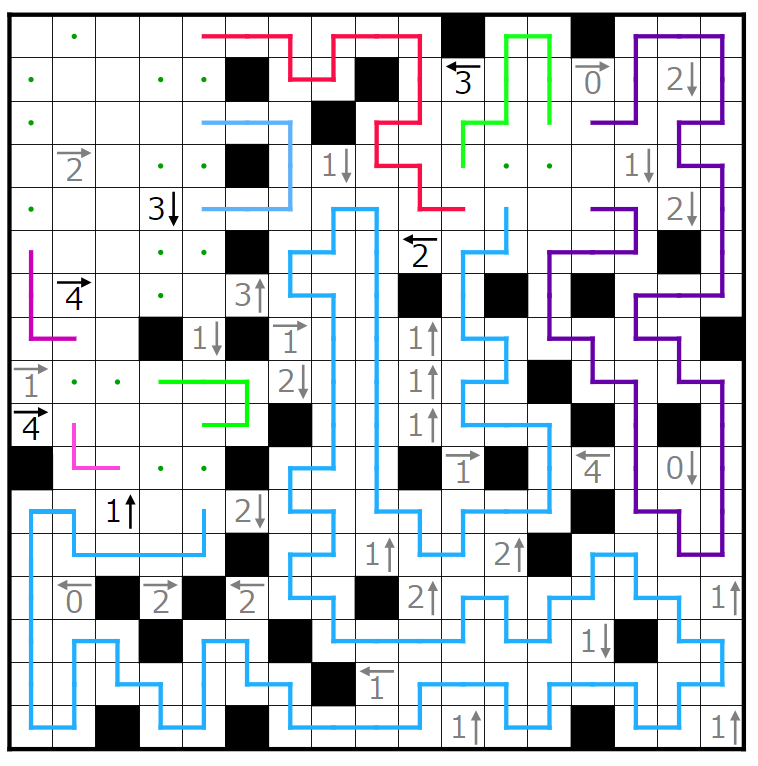
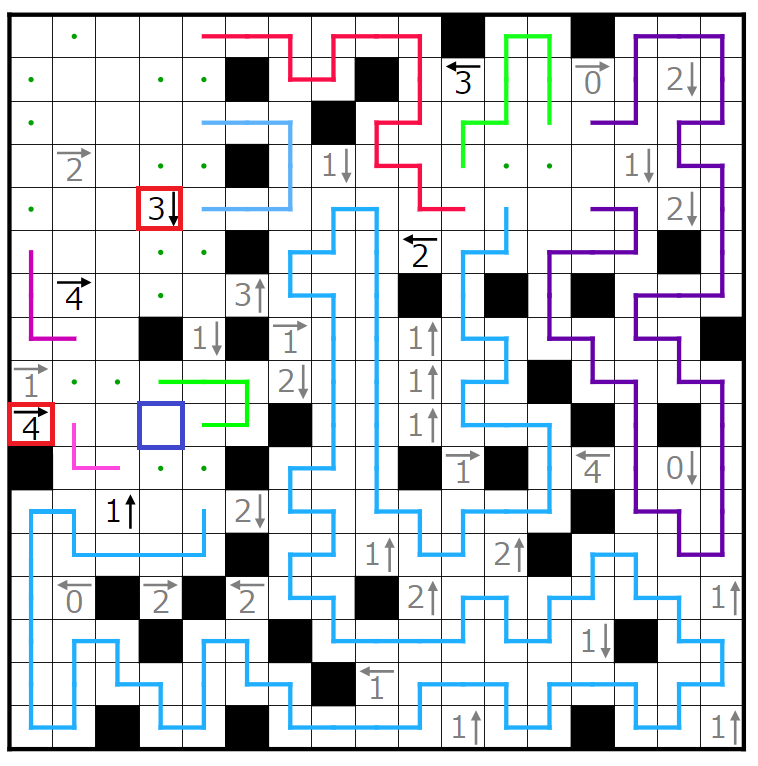
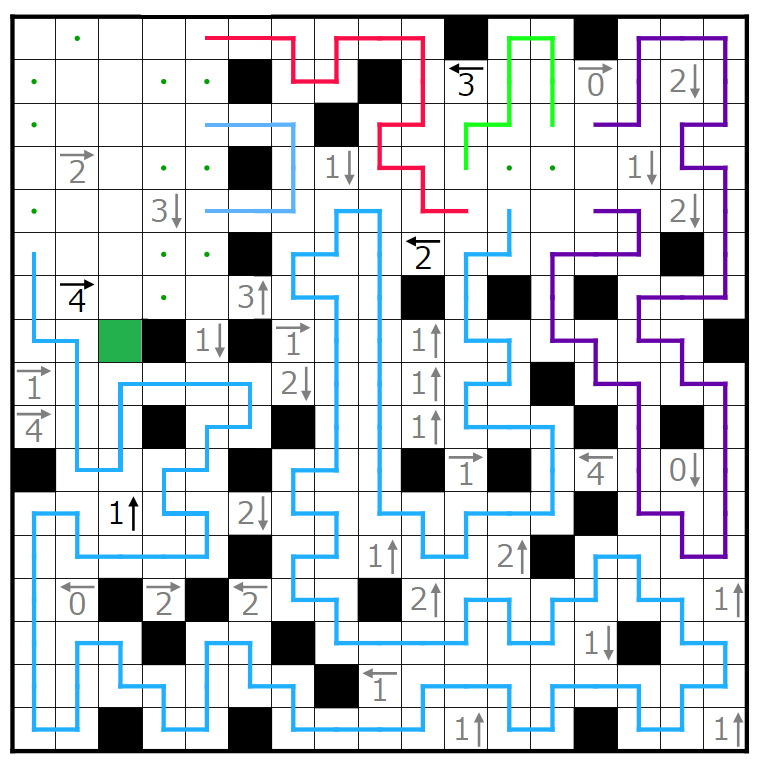
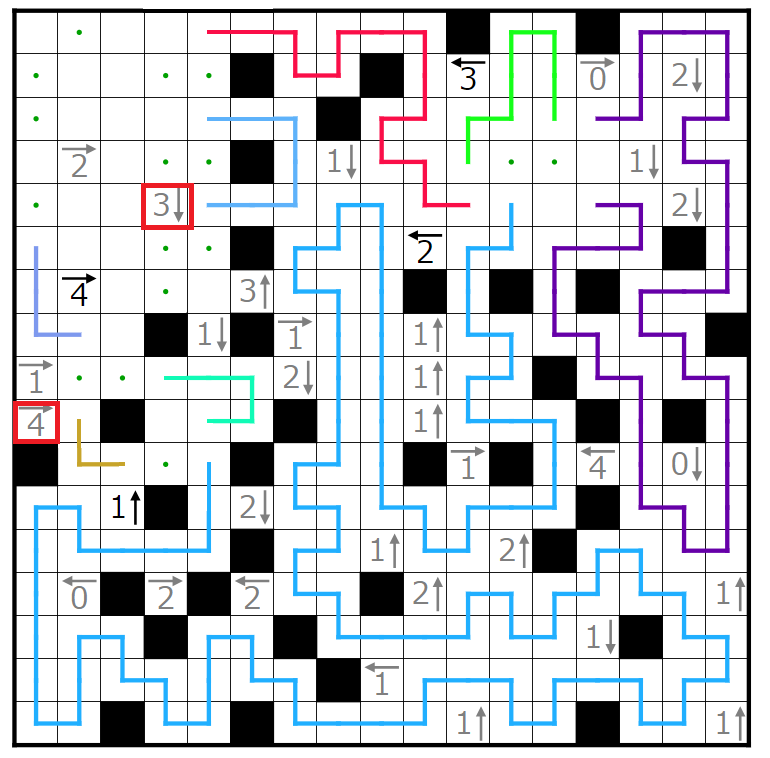
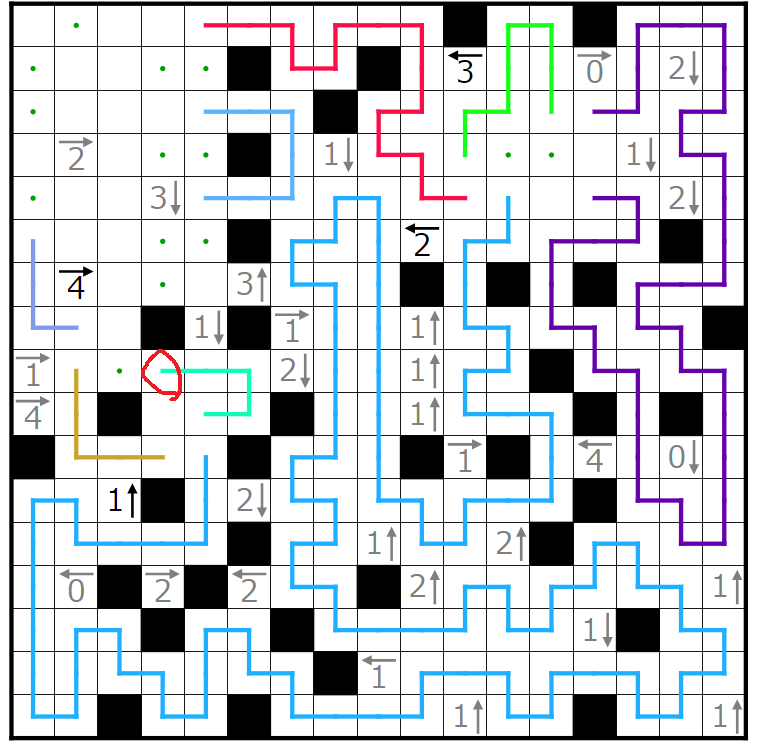
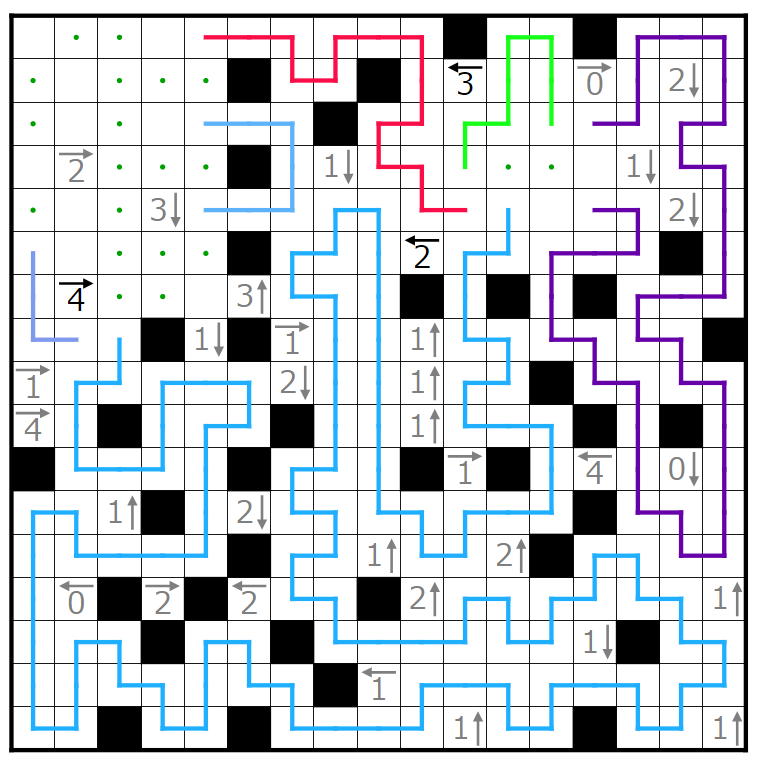
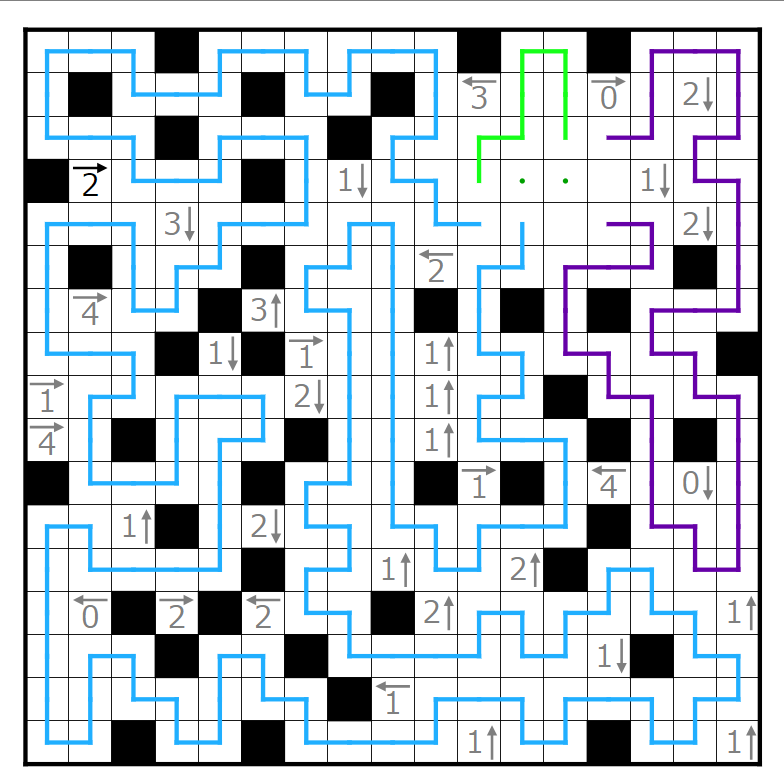
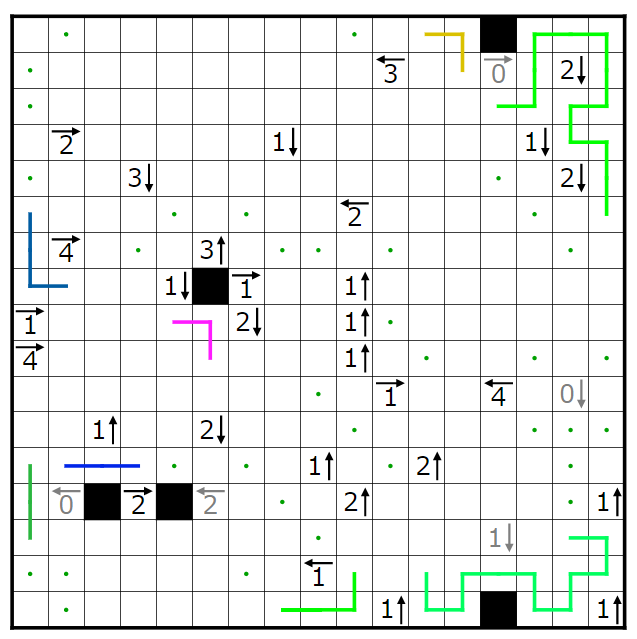
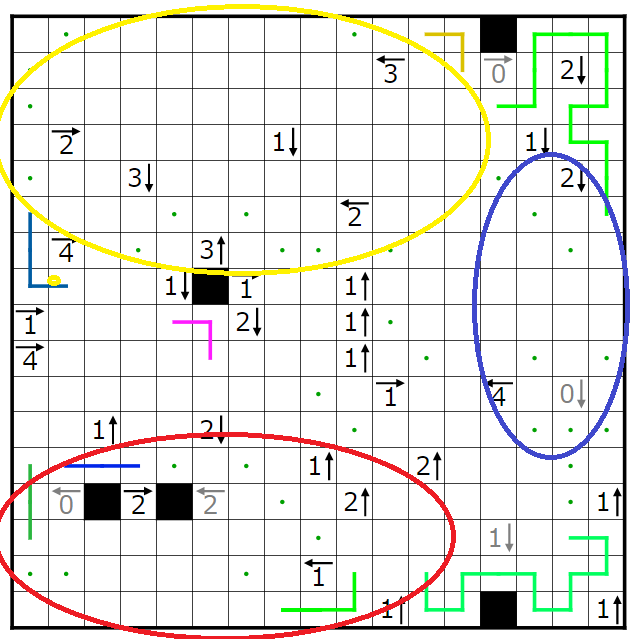
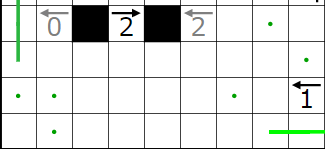
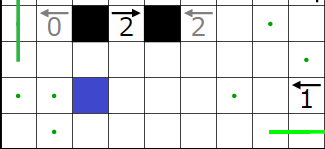
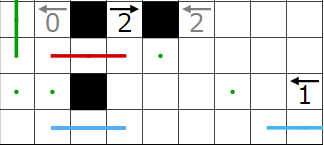
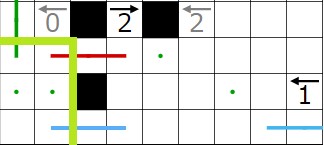
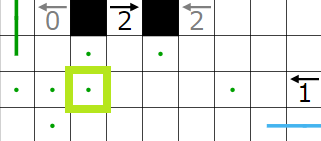
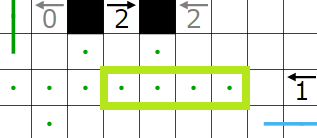
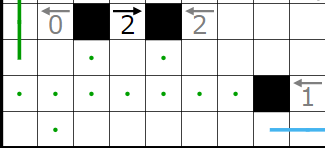
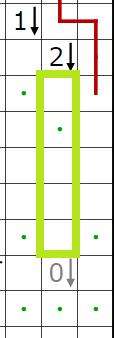
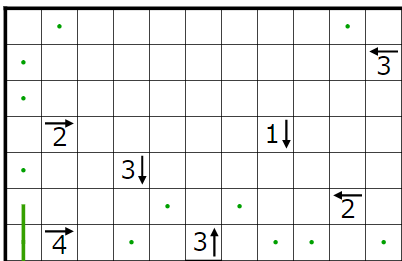
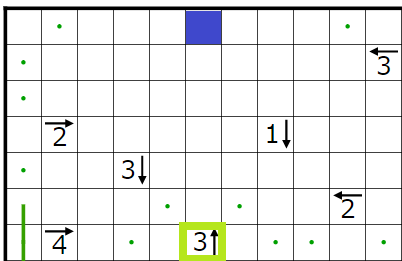
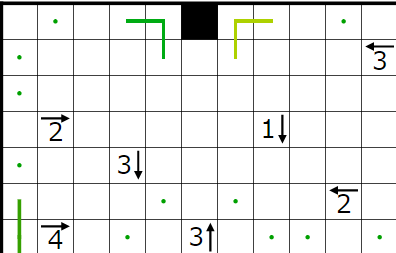
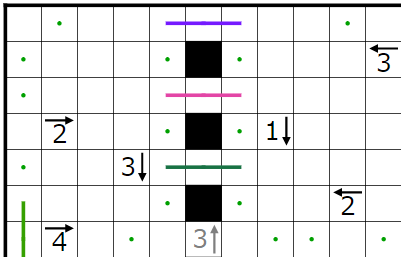
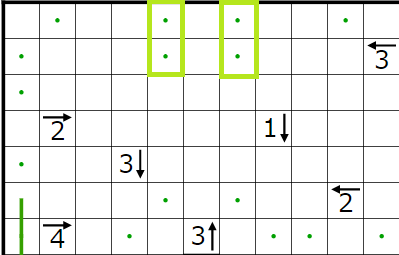
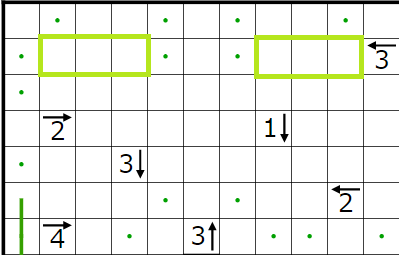
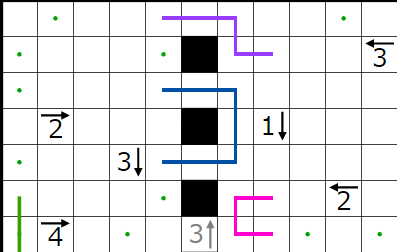
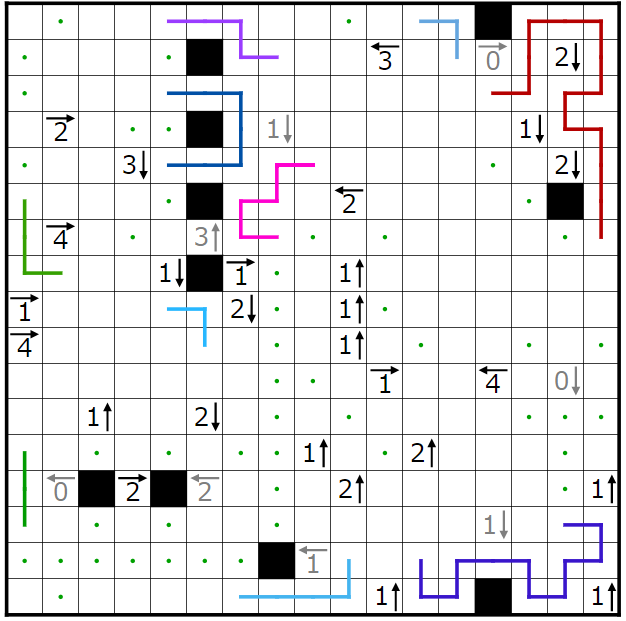
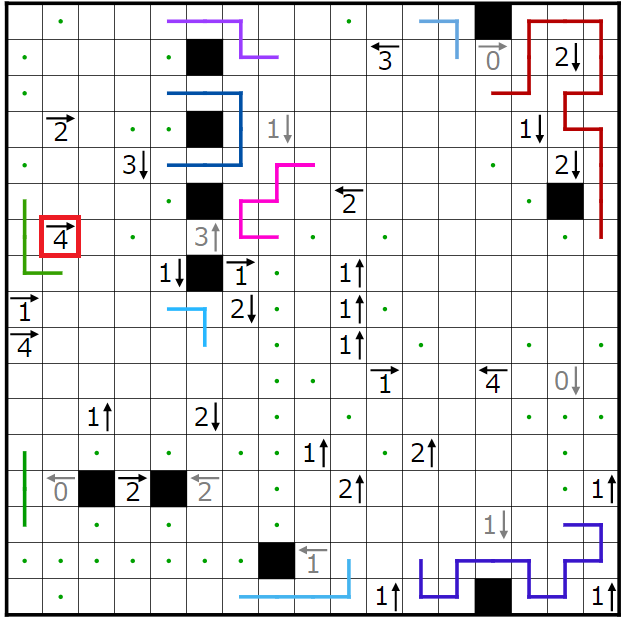
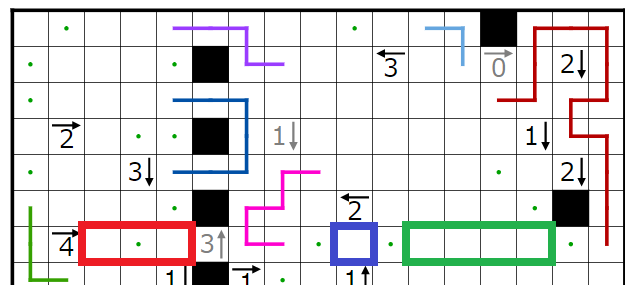
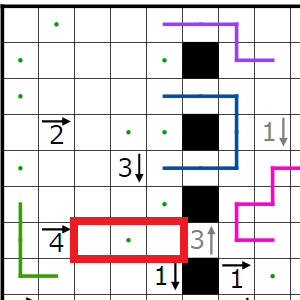
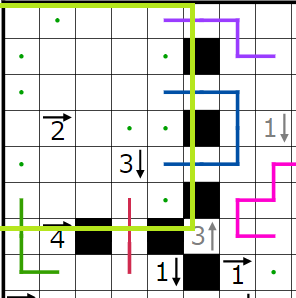
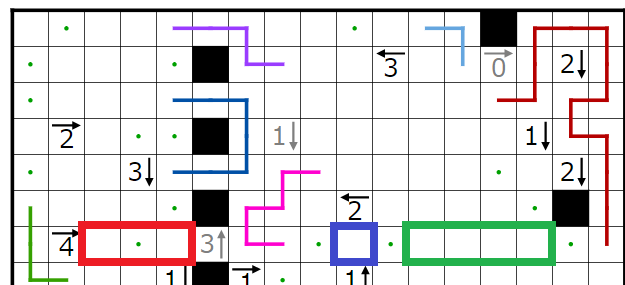
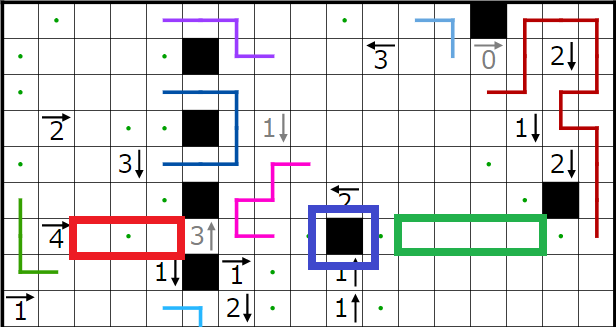
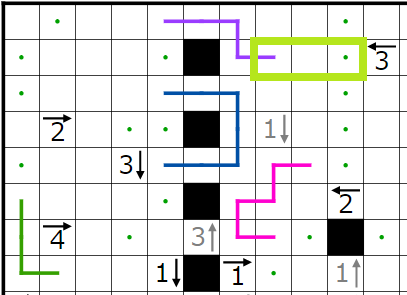
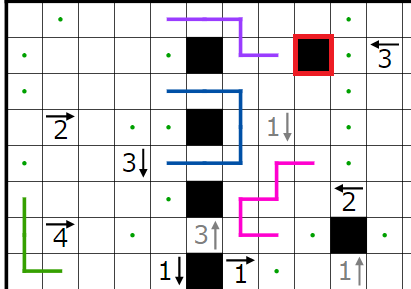
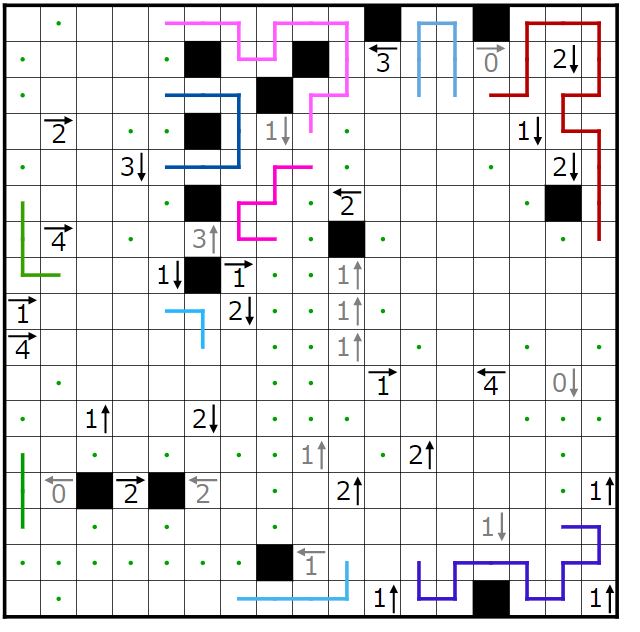
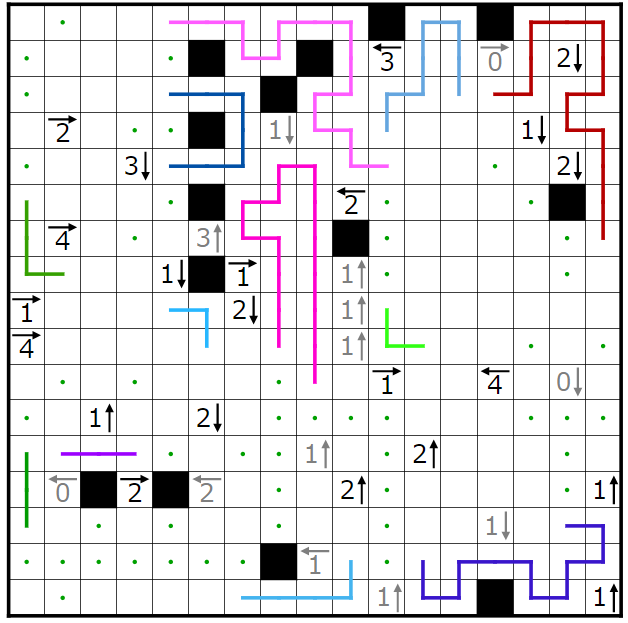
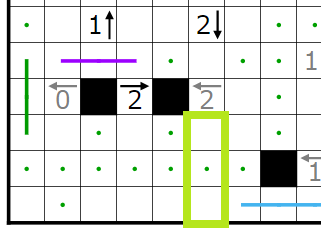
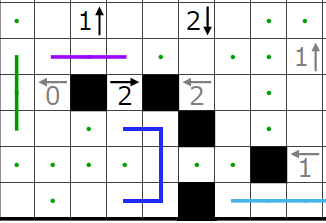
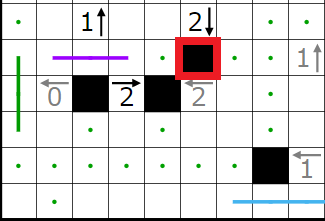
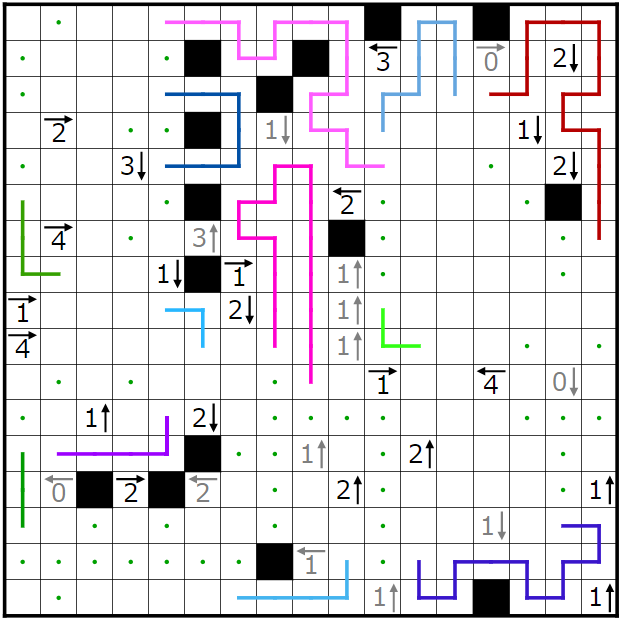
今回の問題

puzz.link/p?yajilin/17/17/l34za42d41m20h22d21d42h43i41h23d12d32h43m12d33d13m31h21d33d40h13i21h40d14d10h32m31d11za43l

優勝 @SP1_winter氏 03分19秒

第2位 @ek_bm氏 03分44秒

第3位 @QUad_R_ANgle氏 03分58秒

第4位 @buyaketa氏 04分34秒

第5位 @ten986氏 04分45秒

第6位 @homerestaurant3氏 04分55秒

第7位 @semiexp氏 05分01秒

第8位 @WrdmntlstIT氏 05分09秒

第9位 @BG_otogame氏 05分15秒

第10位 @4DVector氏 05分42秒

第11位 @flight_float氏 05分44秒

第12位 @pencilkarasu氏 06分18秒

第13位 @Rtz_Satanichia氏 06分35秒

第14位 @0625Master氏 07分27秒

第15位 @bara9598氏 07分33秒

第16位 @heno_code氏 08分02秒

第17位 @kobouzu17氏 08分03秒

第18位 @Daikichi_3141氏 08分24秒

第19位 @bopbobpop氏 08分34秒

第20位 @gonzaemon48氏 08分39秒

第21位 @volxa氏 08分40秒

第22位 @_icchicchi0903_氏 08分51秒

第23位 @1220oz_an氏 09分04秒

第24位 @1345_12a氏 09分12秒

第25位 @men_cotton氏 10分18秒

第26位 @rikkati氏 10分33秒

第27位 @cuber_nazo氏 10分37秒

第28位 @hek293ft氏 11分39秒

第29位 @3v8g氏 12分06秒

第30位 @lifein0ftoxun氏 13分44秒

第31位 @hamayoshi60氏 15分44秒

第32位 @melvy_puz氏 16分29秒

第33位 @b6juka氏 16分44秒

第34位 @20020103e氏 20分48秒

第35位 @inpachi2dx氏 20分51秒

第36位 @Squidlover8po31氏 24分34秒

第37位 @kai1000_don氏 29分02秒

第38位 @As_you_know7911氏 30分28秒

第39位 @fuwa_lica_chan氏 30分38秒

第40位 (๑•﹏•๑｀)ふぇぇ氏 30分47秒

第41位 @Katze_miZki氏 32分21秒

第42位 @tempura_cpp 36分13秒

第43位 @ryosei0627氏 36分43秒

第44位 @puripuri2100氏 41分14秒

第45位 @Pollux33311氏 41分37秒

第46位 @beta_2_beta氏 42分30秒

第47位 @shi20170211氏 48分13秒

第48位 @GalaxxxyToybox_氏 49分25秒

第49位 @pleiades_puz氏 50分48秒

第50位 @kav_to氏 51分11秒

第51位 @a_ka_me_ga_ne 56分48秒

以上になります！！

優勝されたSP1（@SP1_winter）氏おめでとうございます！！！

皆様ご参加ありがとうございました！！！！

閉会の言葉

ご参加いただいた皆様お疲れさまでした！！

今回は過去最高の人数(55名)の方に参加して頂きとても嬉しいです、ありがとうございます！！

今回は、前回の7月②大会は問題がとても難しいということ、①大会で有ること、を鑑みて比較的気軽に解けるように作ろう～と思って気軽に問題を作ってみました。

しかし、自分の解いた問題を解きなおし難易度分類をする、という作業をしている最中に作ったためか、無意識のうちに上級手筋詰め合わせセットみたいな問題になってしまいました。自分のツイッターの難易度評価で言うとやや難しいぐらいかなあと思います。

でも３分ははやいとおもいます（小並感）

・

次回大会は8月28日（水）の22時からの予定です！

それでは皆様ご参加ありがとうございました！！！

今回の問題

puzz.link/p?yajilin/17/17/d32c3241p31e22u32a41a24a2120r12k24b43a26f23a11zs23a12a21d32l2222g41c12h40r33c41b2121f40zx33g

【お題】

何かと話題の映画「天気の子」。
それでは、次にキそうな〇〇の子は何か教えて下さい。

 

【最優秀回答】

数の子 (ラマヌジャン的な)

 

→ お正月あたりにくるかもしれませんね！（違う）

 

 

【優秀回答】

天気の子の子

→ 孫！

 

近畿

→ 天気キッズ！

 

大河ドラマ「朕の子」

→ 変な事はもちろん何も言ってません。

 

 

【その他】

この猫箱根の子

このねこはこねのこ

→ お見事！

 

 

本格焼酎かんのこ

唐辛子などに漬け込んだスケトウダラの子

→ 酒とつまみが揃ってしまいました。

 

 

木の子vs竹の子

→ 私はガルボ派です！

 

 

夏の省エネ促進キャンペーン

「私、好きだな、この仕事 電気の仕事 私ね、自分の役割みたいなものが やっとわかった」

東京電力と天気の子がコラボレーション！

《電 気 の 子》

→ そういえばでんこちゃんって元気なんですかねえ。 

 

---

【おまけ・拙作】

落合博満

岡本かの子

も～…あっ、そういえばさ、あの子俳優になったんだって！んでこないだやってた映画に出てたらしいのよ～ね～本当よ～誰って？もう嫌ね～ほら～いつも来てたじゃないあのタンクトップの子

を散らすように蜘蛛の子（倒置）

便秘

点P

円C

メンディー

ビアンカ

ひろみちお兄さん

東京ひの子

はいだしょうの子

滝川クリステルジュニア

前編はこちら

→aoiatuage.com/archives/495

忘れたところなどを書き加えていますが、前編ではここまで進みました。

---

 

次にこの４←ヒントに注目したいと思います。

---

 

次に、赤四角で囲んだヒント群に関して、青四角のマスに黒マスが入らないと仮定してみます。

以上より、どのように黒マスを置いても矛盾することが示せたため、初めの青マスに黒マスが入らないという仮定がおかしいことが分かったため、青マスの部分に黒マスが入ることがわかりました。

---

そこから少し決まるので決めていきます。

---

 

---

 

---

 

次に赤四角で囲まれた２↓のヒントを考えます。

---

以下、順当に伸ばしていきます。

---

 

右下の閉空間に入り込む線の端の偶奇を考えれば、赤丸の線の端は上に行くことが分かります。

右下の閉空間において、青丸で囲まれた線の端をくっつけると右側水色の線のループが孤立してしまうことが分かります。よって青丸で囲まれた線の端はくっつけないように伸ばします。

左上の閉じた空間を考えると赤く囲まれた線の端は左に行くことが分かります。

ここまで埋まりました。

次に、緑で囲んだ４→のヒントに注目します。すでに２個黒マスがあるため赤四角と青四角の部分に計２個黒マスが入ることになります。

今、赤四角に２個黒マスを入れると仮定します。

 

少なくとも囲んだ閉区間に線の端が奇数本であるため矛盾します。

よって赤四角、青四角にはそれぞれ黒マスが１個ずつ入ることが分かり、特に青四角のマスには黒マスが入ることが分かります。

ここまで埋まりました。

---

さて、終盤です。作っているときは残りの部分が簡単に決まらなければいいやぐらいの気持ちでとりあえず簡単に決まらないパターンを探して採用した感じだったからかややこしい気がします。

この３↓のヒントに注目します。

解説は以上になります。長くなりましたが、ここまで読んで頂きありがとうございました！！

　前回開催させて頂きました７月早解き大会②（ヤジリン）の問題が難しく、解説が欲しいと要望がありましたのであくまでも自分の解き方ではありますが解説させて頂きます。

puzz.link/p?yajilin/17/17/za33b40a22s42e21f21e23k22j32h44c13o21a41b11g41e22b11g44h11q41b34a20c11b22s11b12f30a42a32c12f11m21k31r11e11

↑問題はこちら

 

---

 

とりあえず単純仮定等々で決まるところまで埋めてみました。点・は黒マスが入らなく線が通るマスであることを表します。

左下、右、左上の順に説明します。

左下

右

左上

　とりあえず今まで決まったところと、１↓のヒントによって決まる点・を打ったところです。

　余談ですが、今回の問題は０のヒントでバーッと点・を最初に打たれるよりも１のヒントを使って、あるところが解き進んでから気づかないと点・が打てないようにしたら時間が稼げるんじゃないかなーと思ってそういう１を意識的に入れるようにしてみました。

---

 

　次に、赤四角で囲まれた４→について考えます。

以上のことから決まるところと、１↑のヒントより確定するところを埋めた図です。

 

 

左下の２↓が一部決まるのを言い忘れていたので解説します。

ここまで確定しました。

---

前編はここまでです。後編はまた後日書きます。