前編はこちら
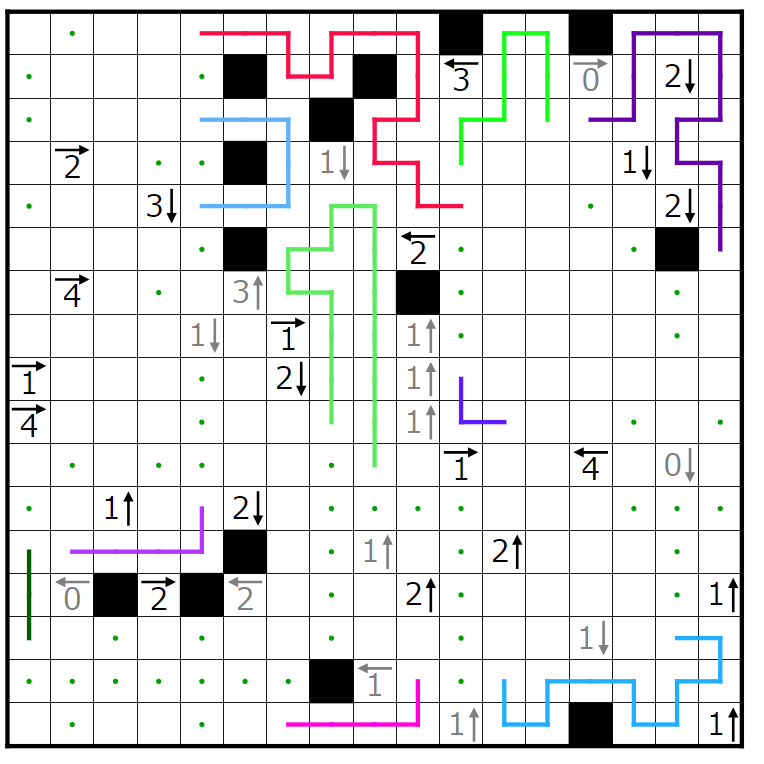
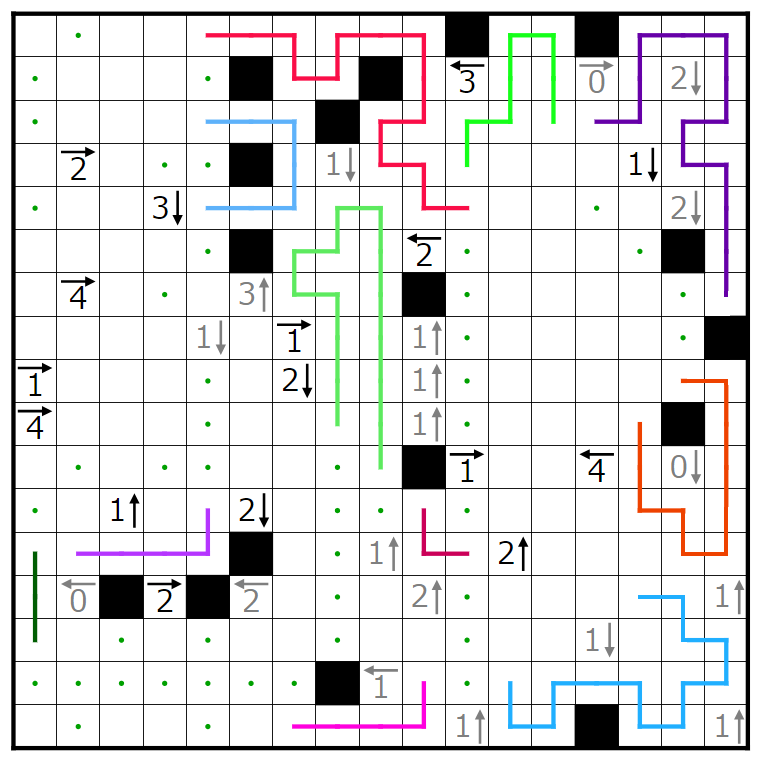
忘れたところなどを書き加えていますが、前編ではここまで進みました。
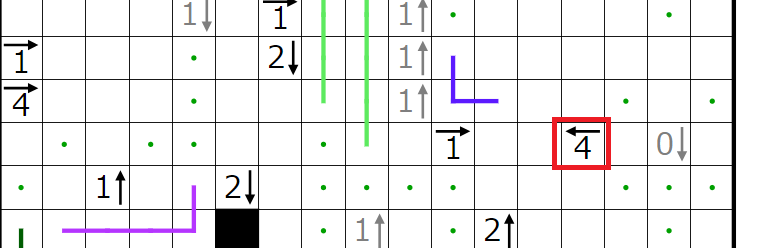
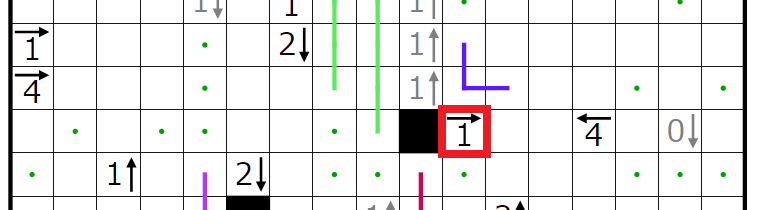
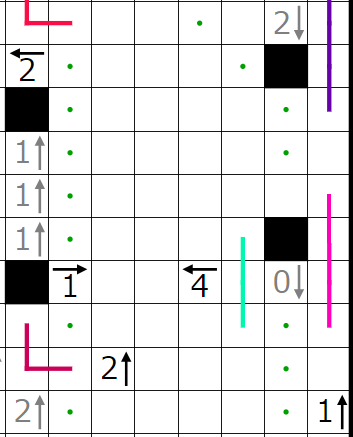
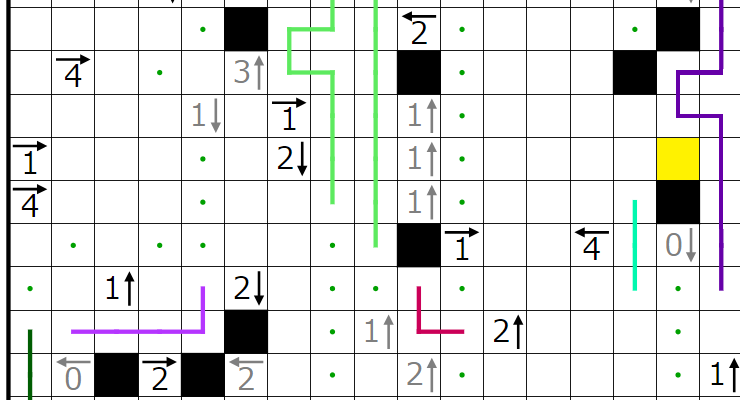
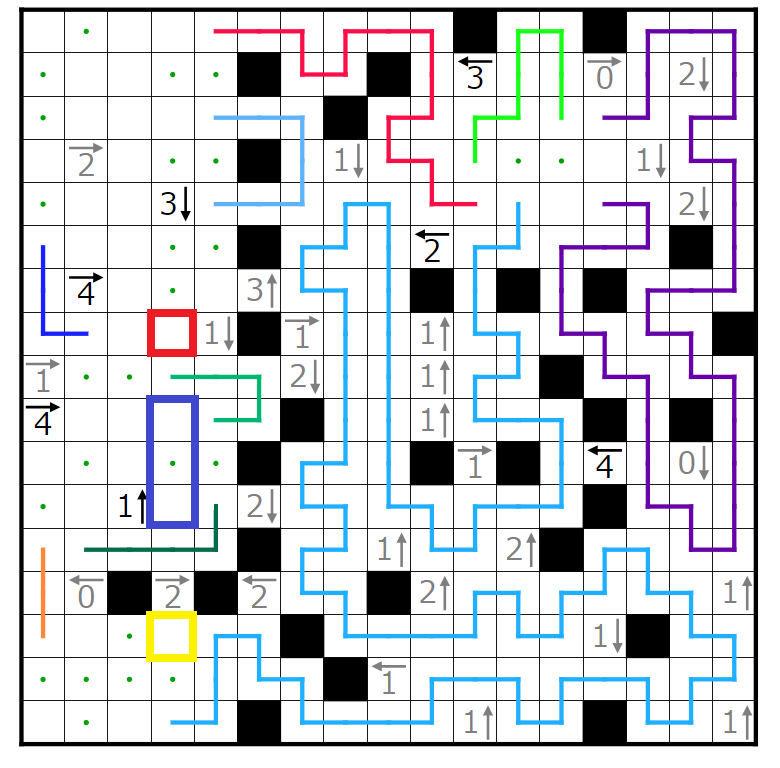
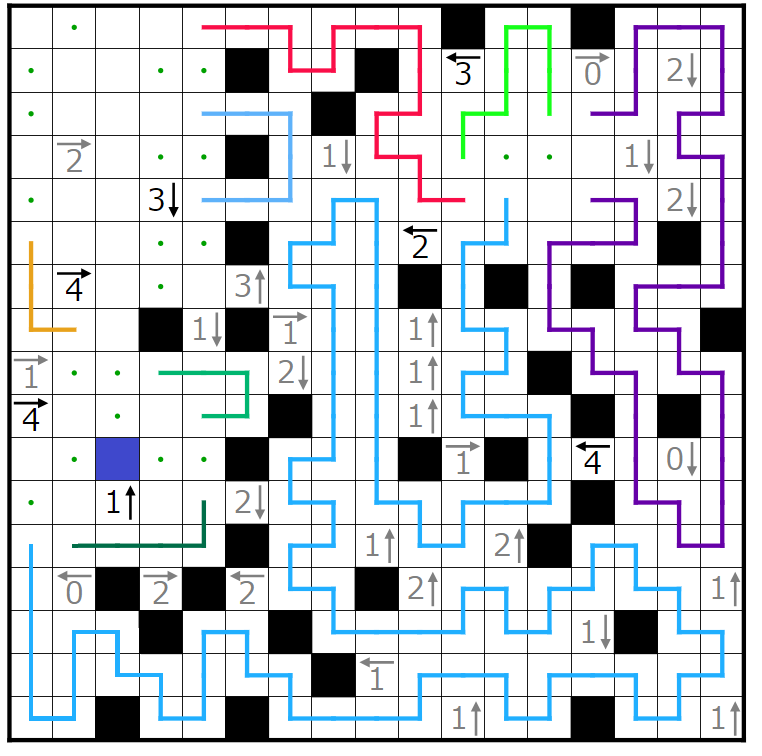
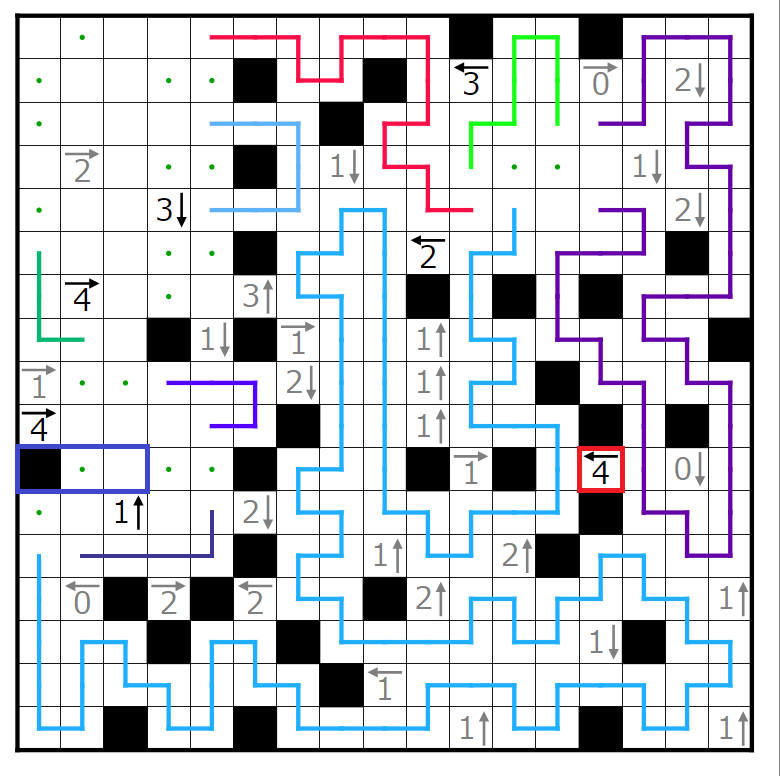
次にこの4←ヒントに注目したいと思います。
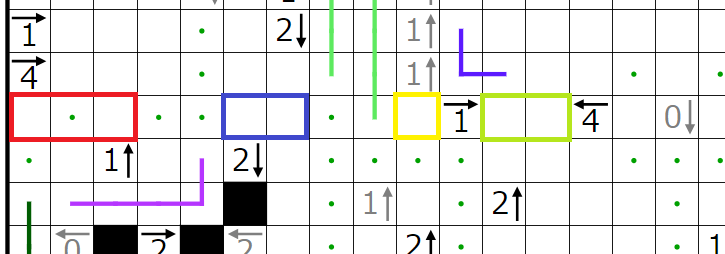
赤四角の部分には2個、
青四角の部分には1個、
黄四角の部分には1個、
緑四角の部分には1個
入ることが分かります。いまここでは特に赤四角の部分に黒マスが2個入ると仮定してみます。
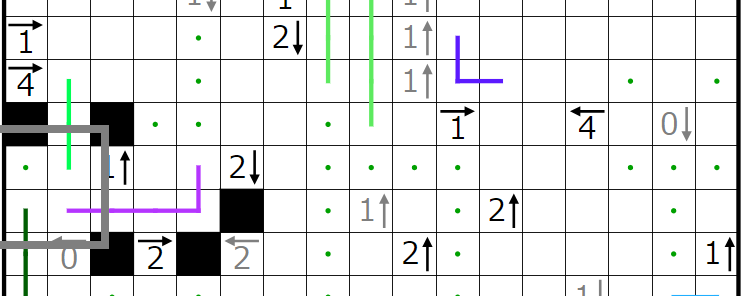

赤四角の部分には1個、
青四角の部分には1個、
黄四角の部分には1個、
緑四角の部分には1個
入ることが分かります。
よって、4←のヒントより、それぞれの部分に1個ずつ黒マスが入ることがわかります。
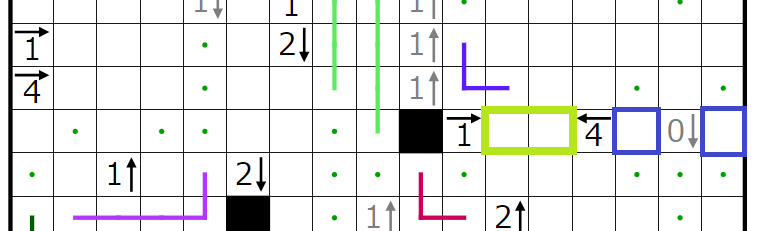
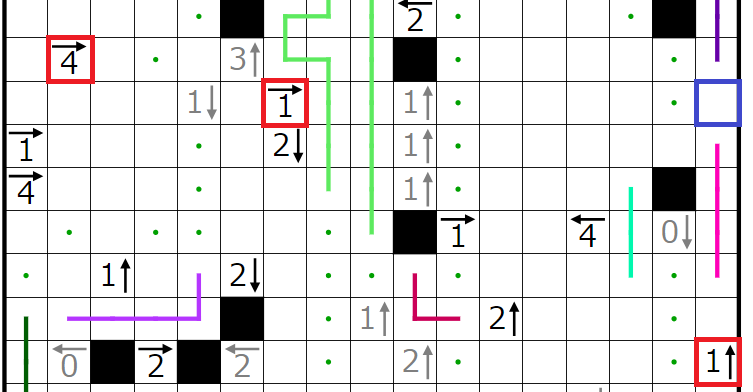
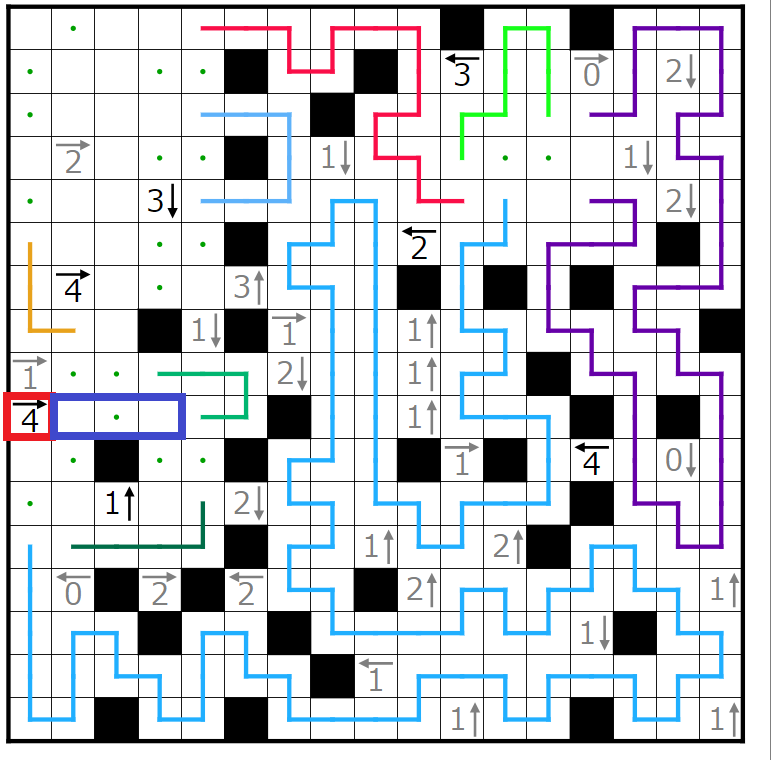
次に、赤四角で囲んだヒント群に関して、青四角のマスに黒マスが入らないと仮定してみます。
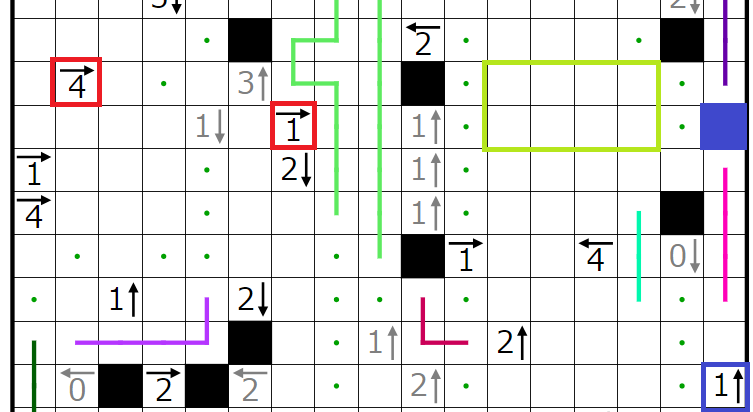
4→の行には2個、
1→の行には1個
黒マスが入ることになります。
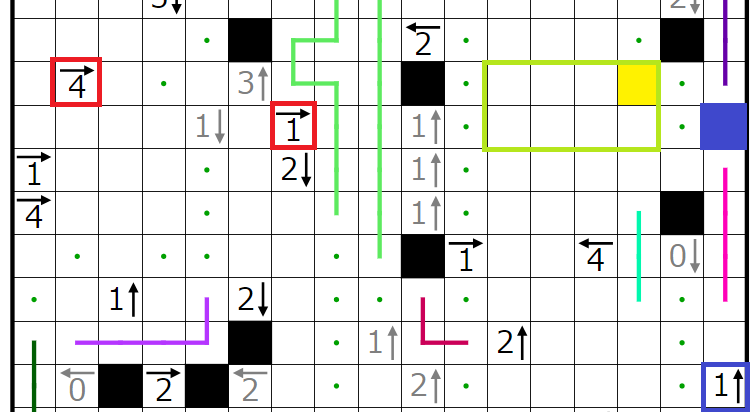
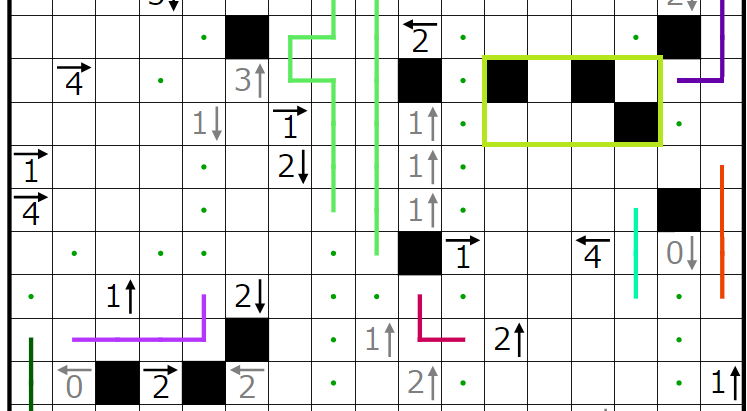
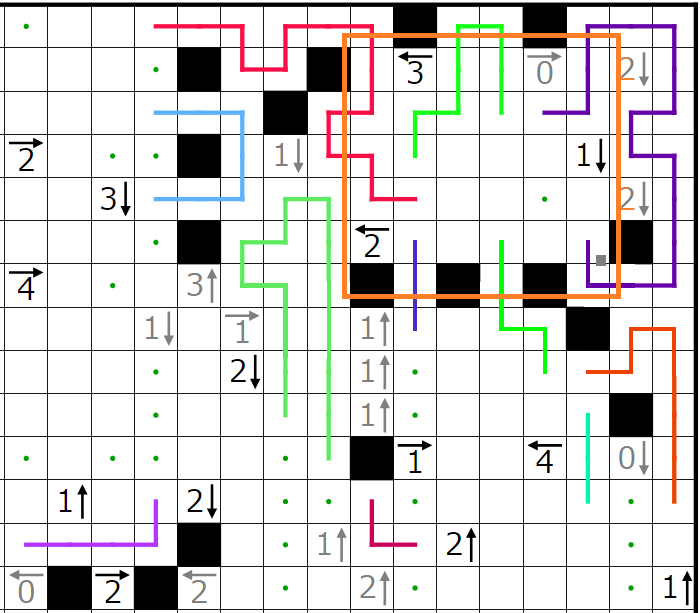
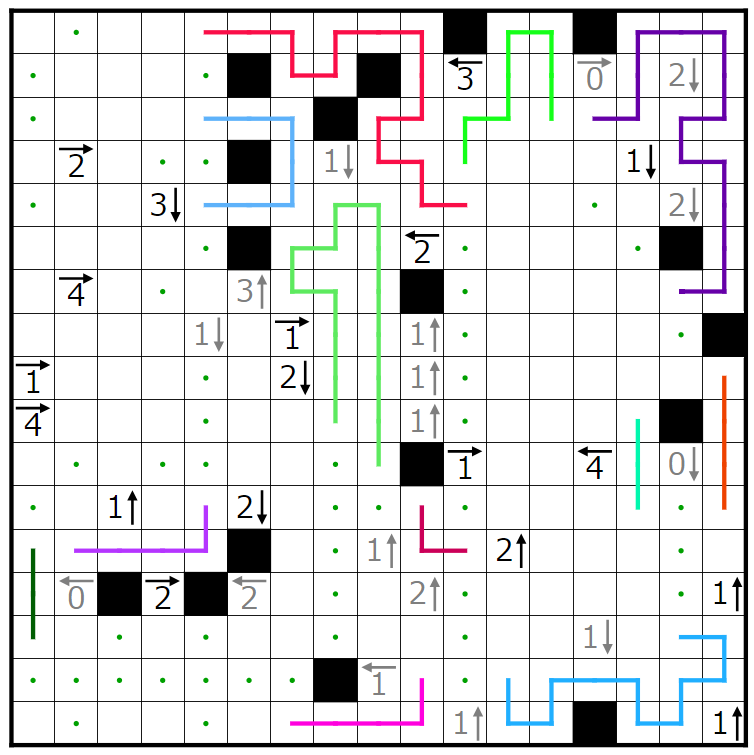
以上より、どのように黒マスを置いても矛盾することが示せたため、初めの青マスに黒マスが入らないという仮定がおかしいことが分かったため、青マスの部分に黒マスが入ることがわかりました。
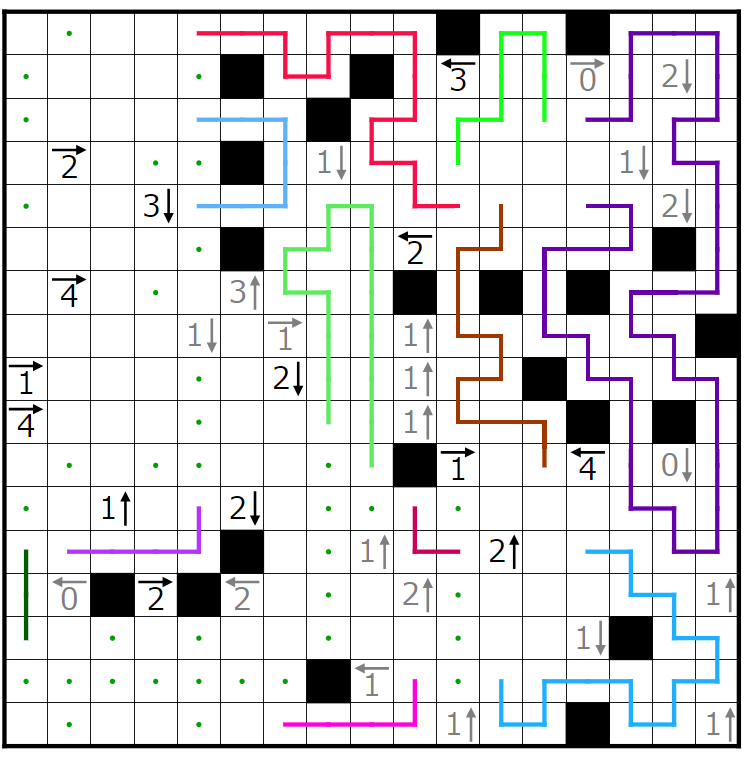
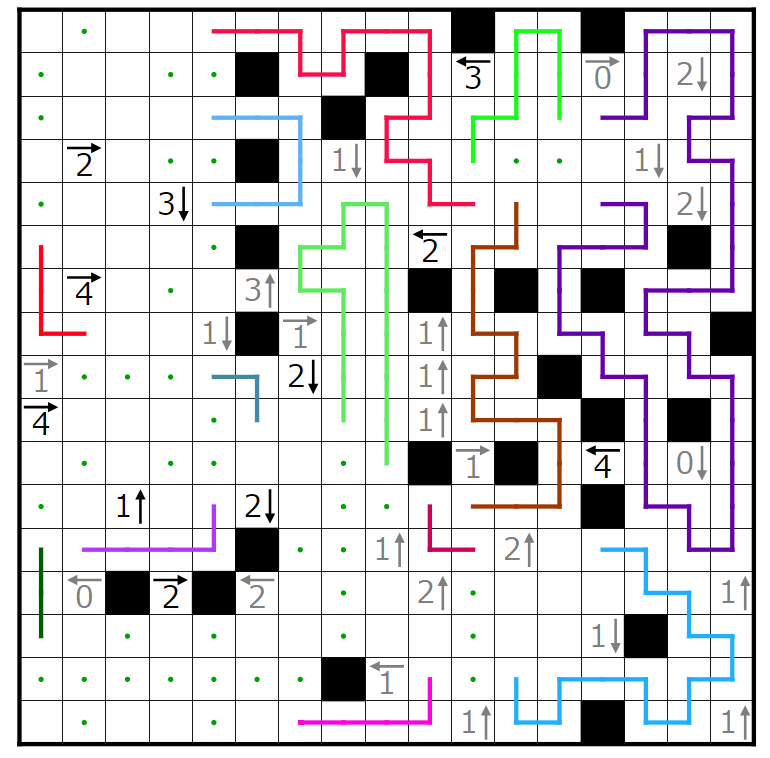
そこから少し決まるので決めていきます。
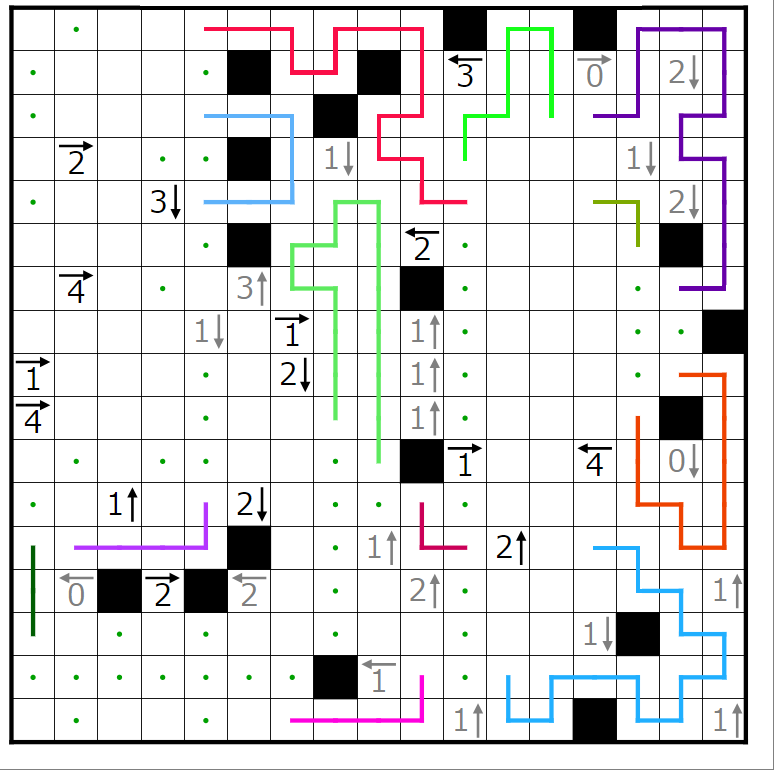
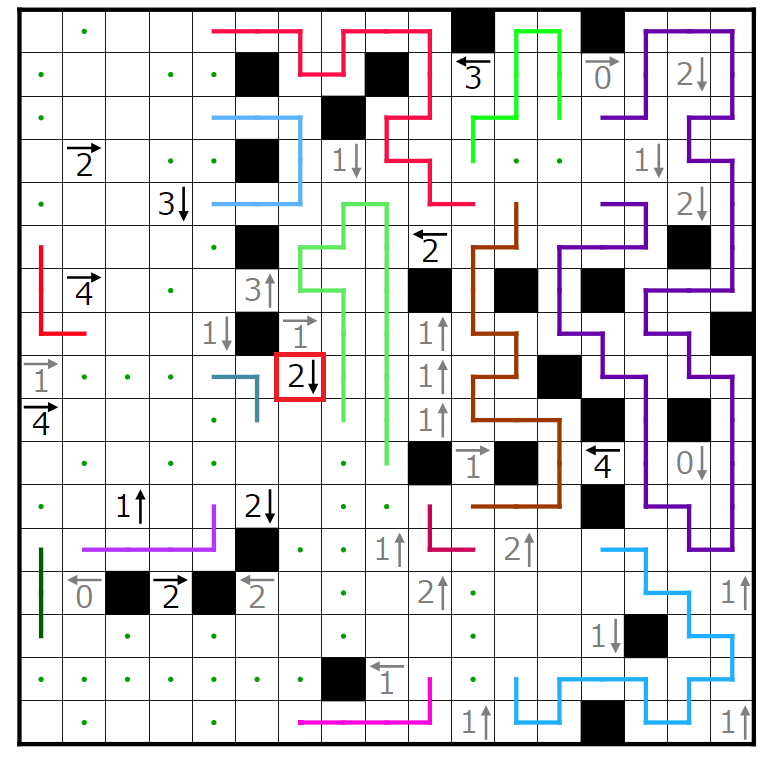
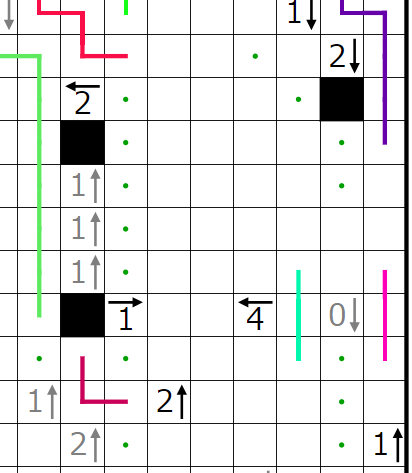
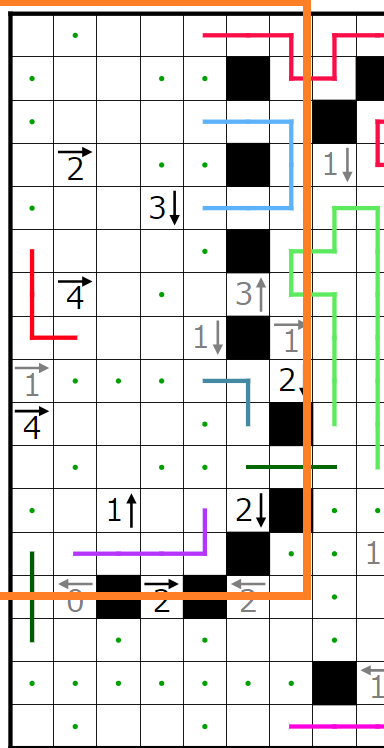
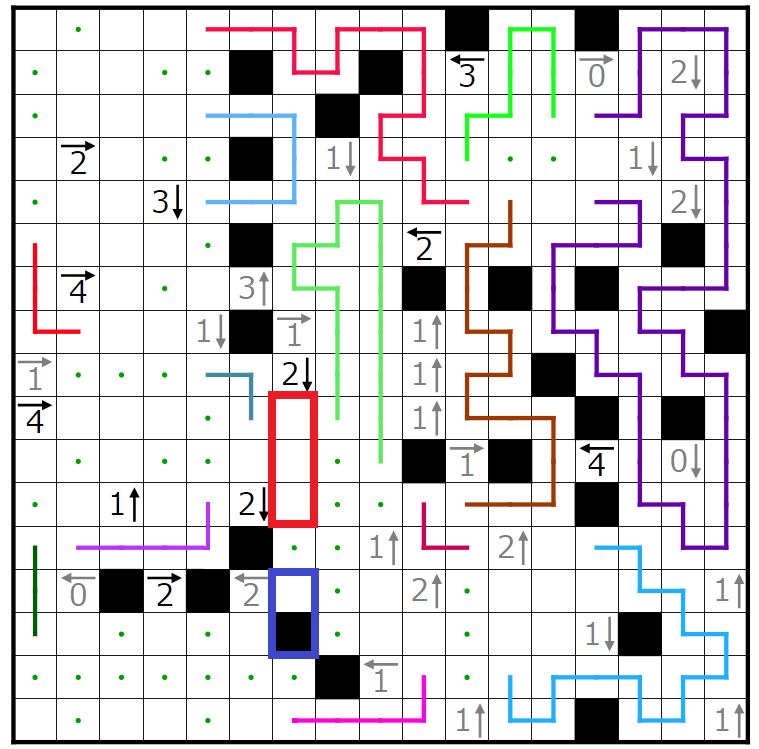
次に赤四角で囲まれた2↓のヒントを考えます。
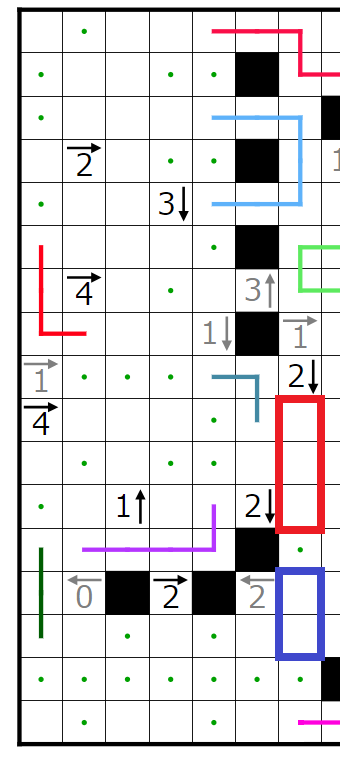
赤四角の部分には2個
青四角の部分には1個
入ることが分かります。
今ここでは赤四角の部分に黒マスが2個入ると仮定します。

赤四角の部分には1個
青四角の部分には1個
入ることが分かります。
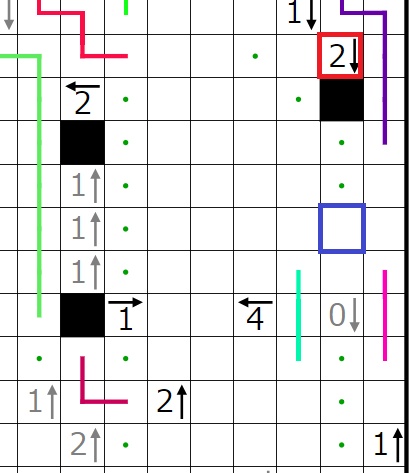
2↓のヒントより、赤四角青四角それぞれに1個ずつ黒マスが入ることが分かります。
次に青四角の2マスのうちどちらに入るかを考えます。
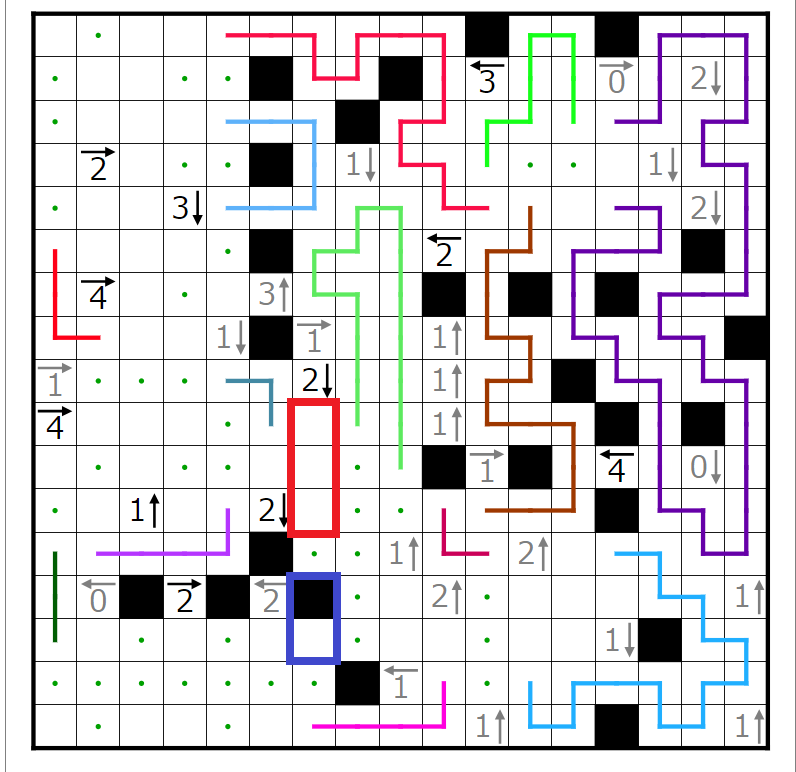
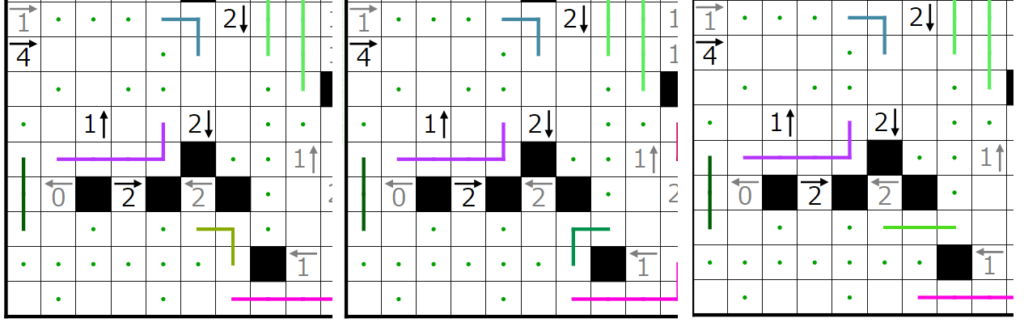
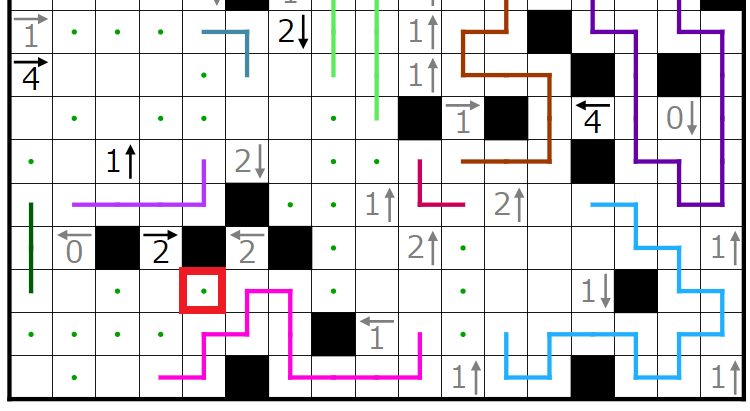
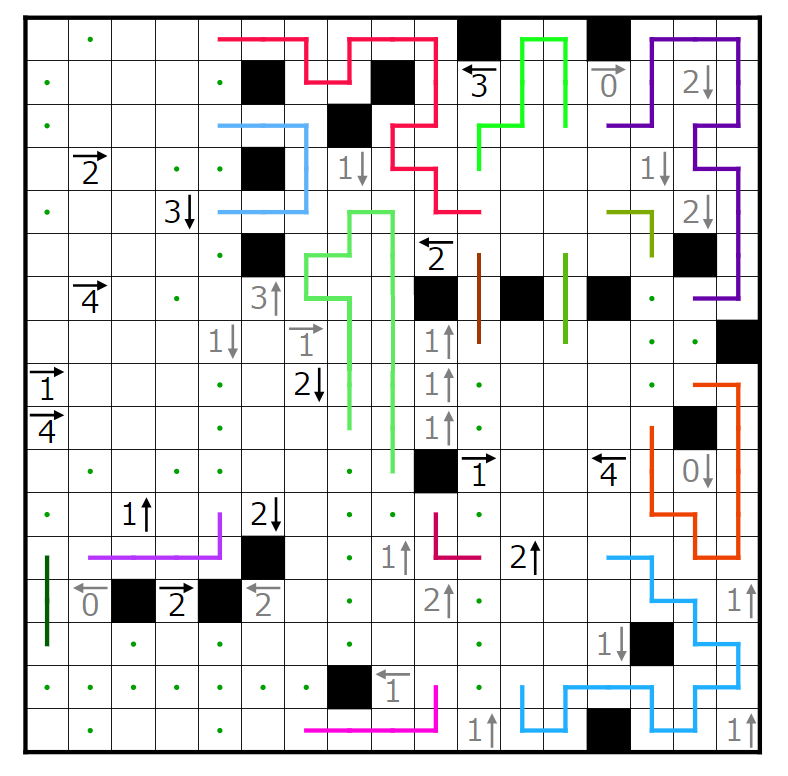
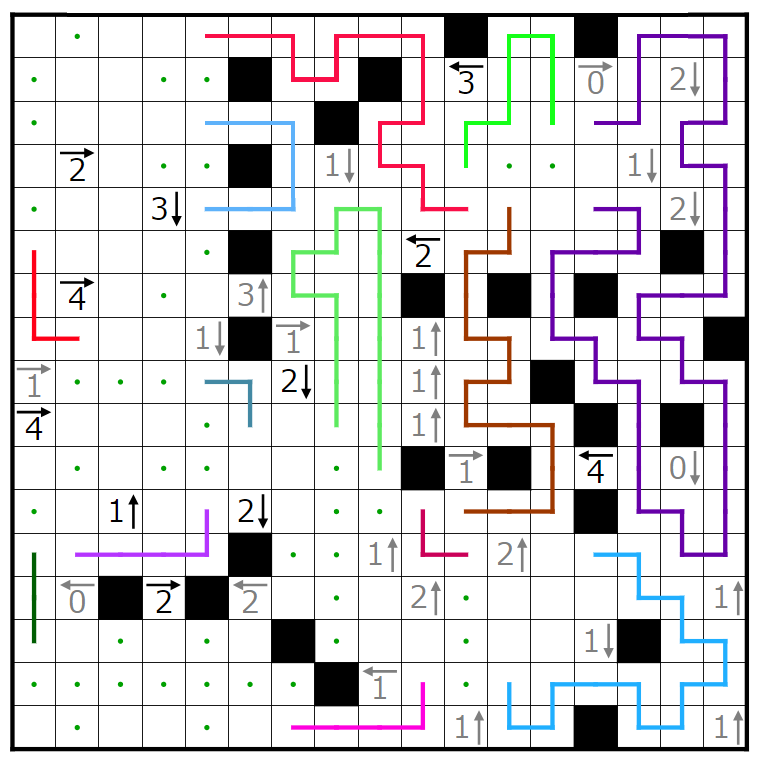
以下、順当に伸ばしていきます。
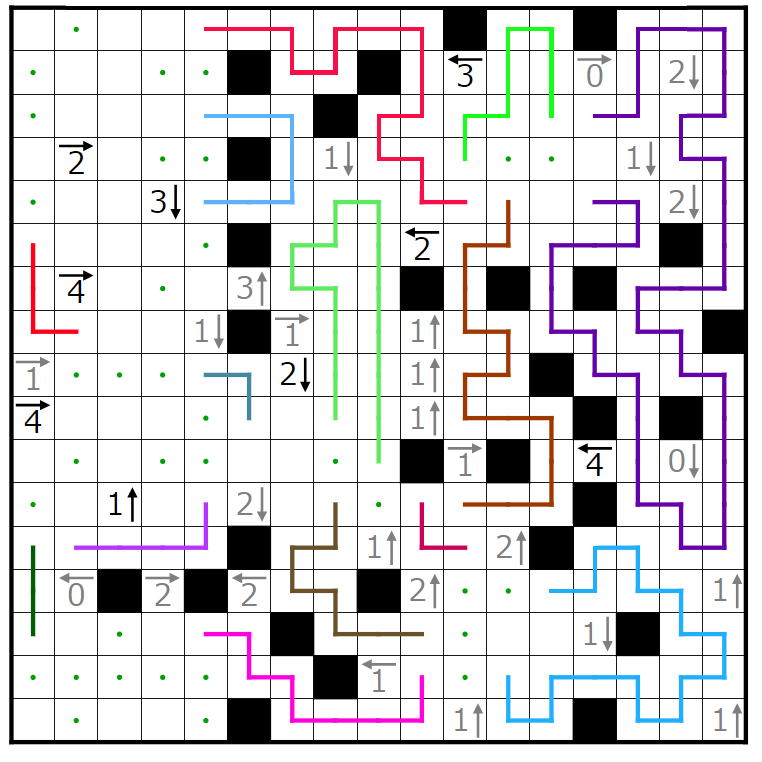
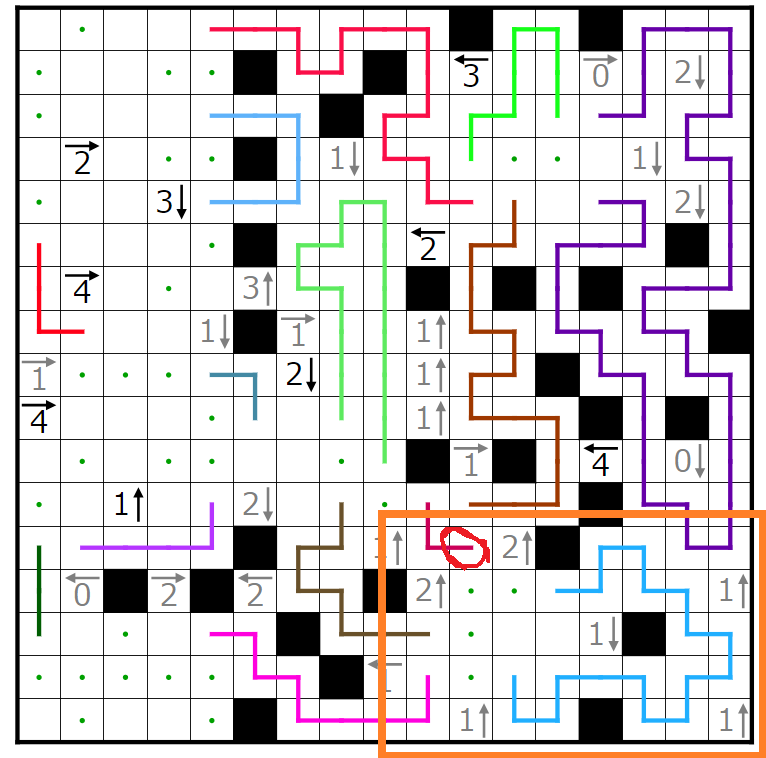
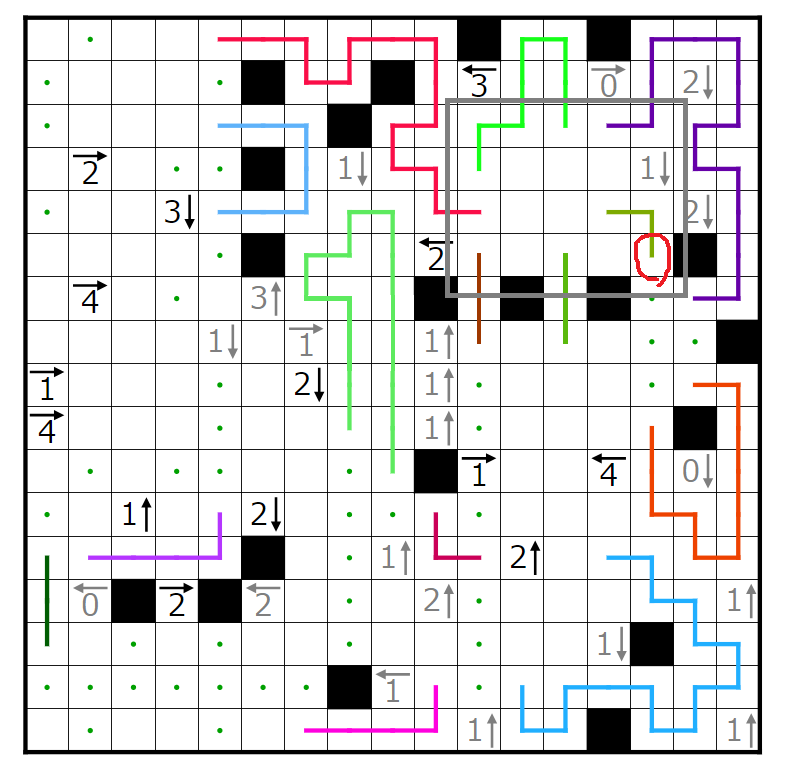
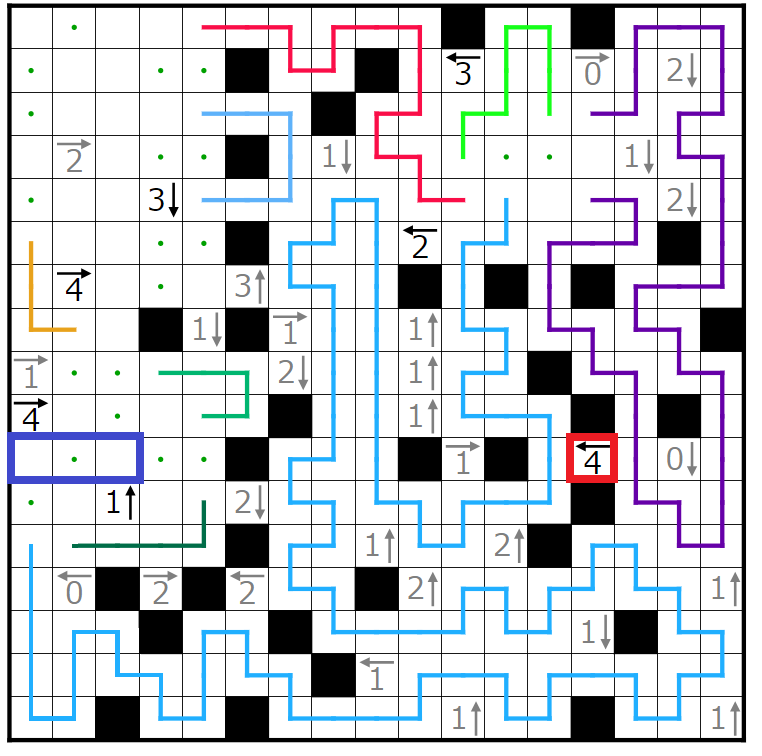
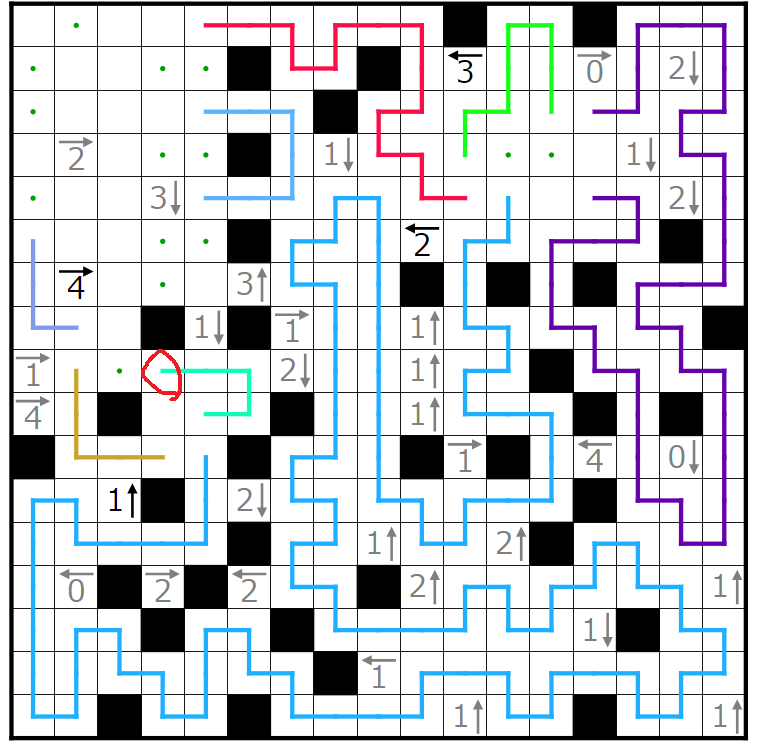
右下の閉空間に入り込む線の端の偶奇を考えれば、赤丸の線の端は上に行くことが分かります。
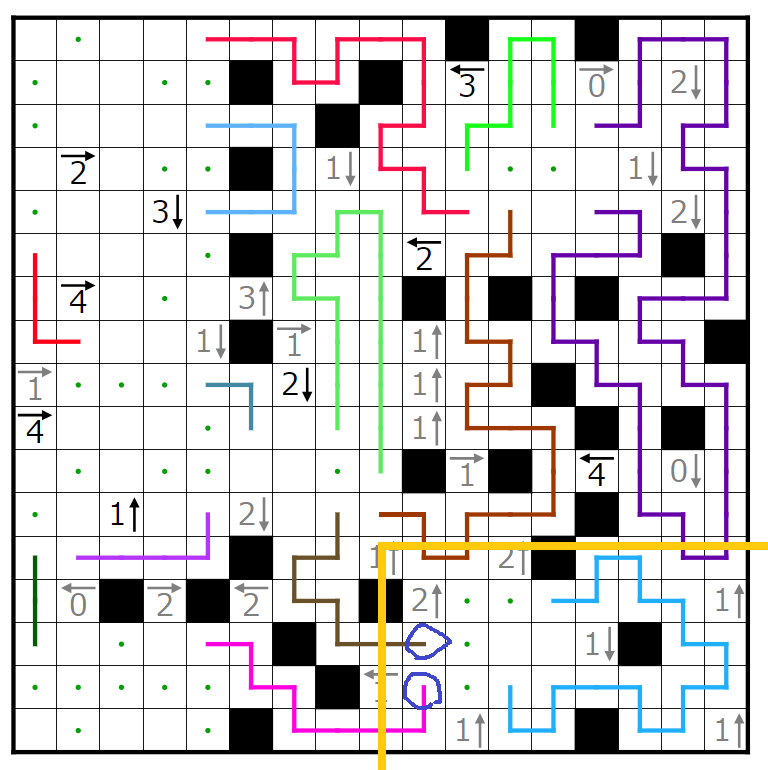
右下の閉空間において、青丸で囲まれた線の端をくっつけると右側水色の線のループが孤立してしまうことが分かります。よって青丸で囲まれた線の端はくっつけないように伸ばします。
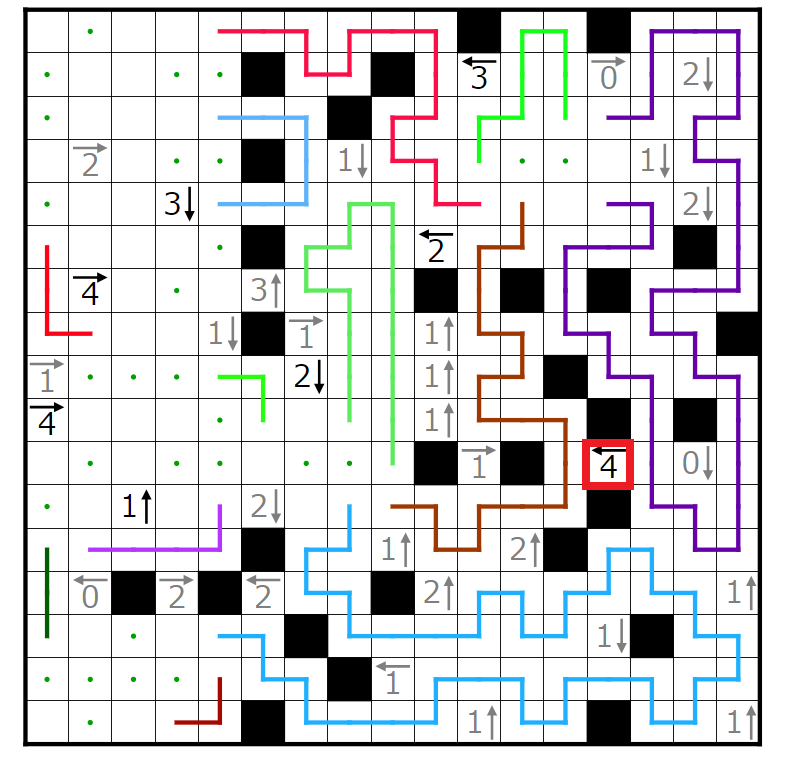
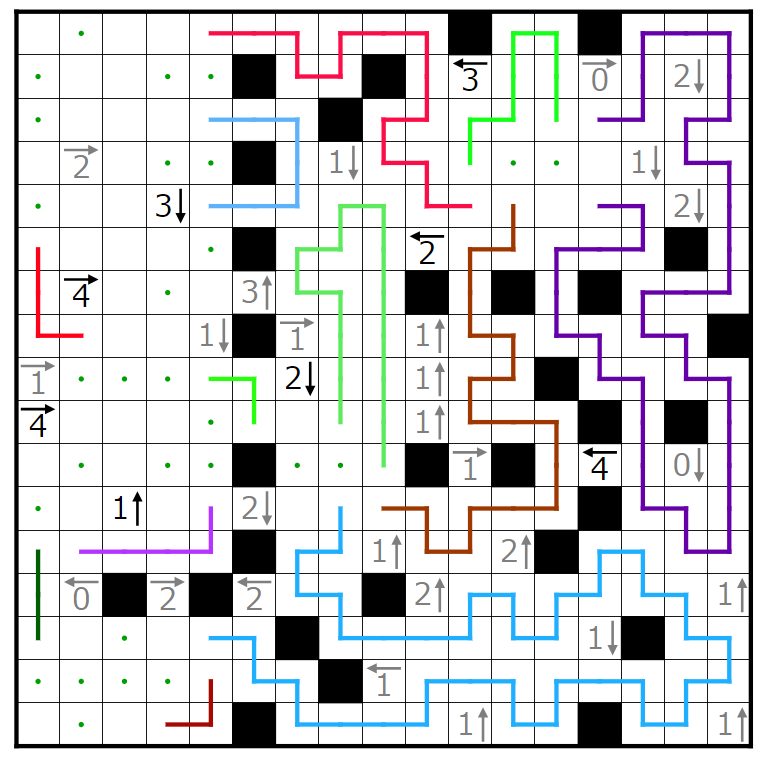
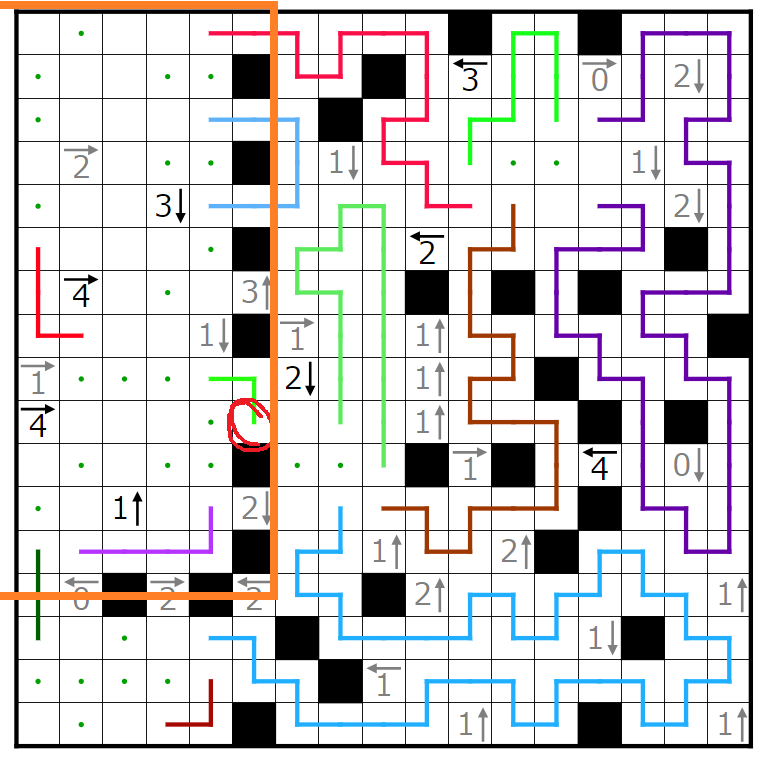
左上の閉じた空間を考えると赤く囲まれた線の端は左に行くことが分かります。
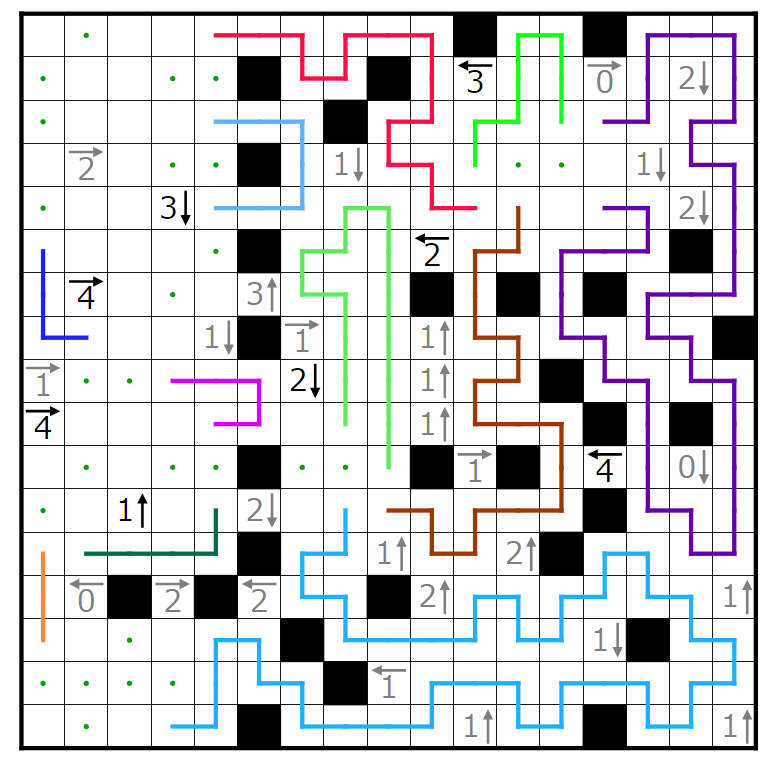
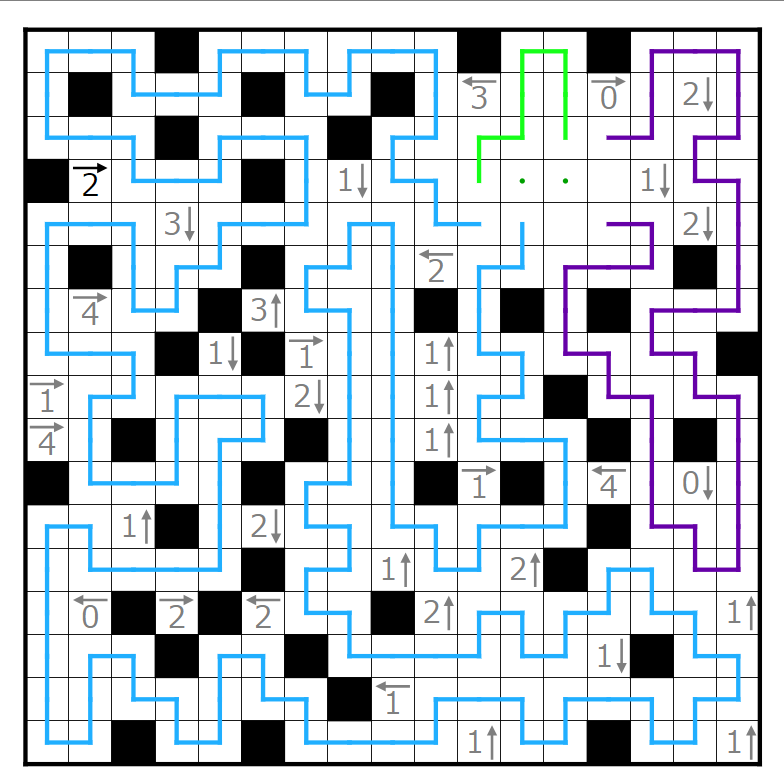
ここまで埋まりました。
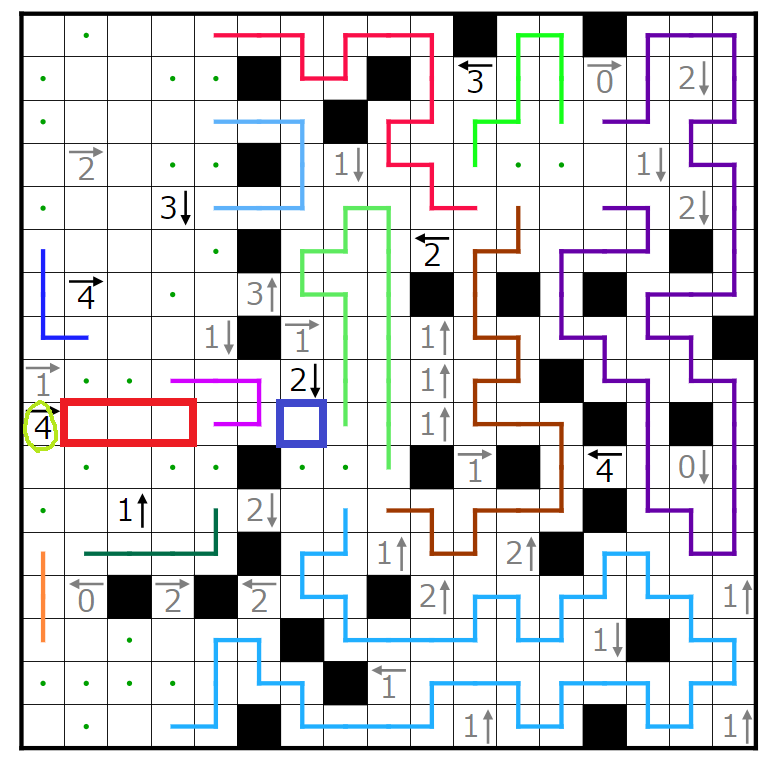
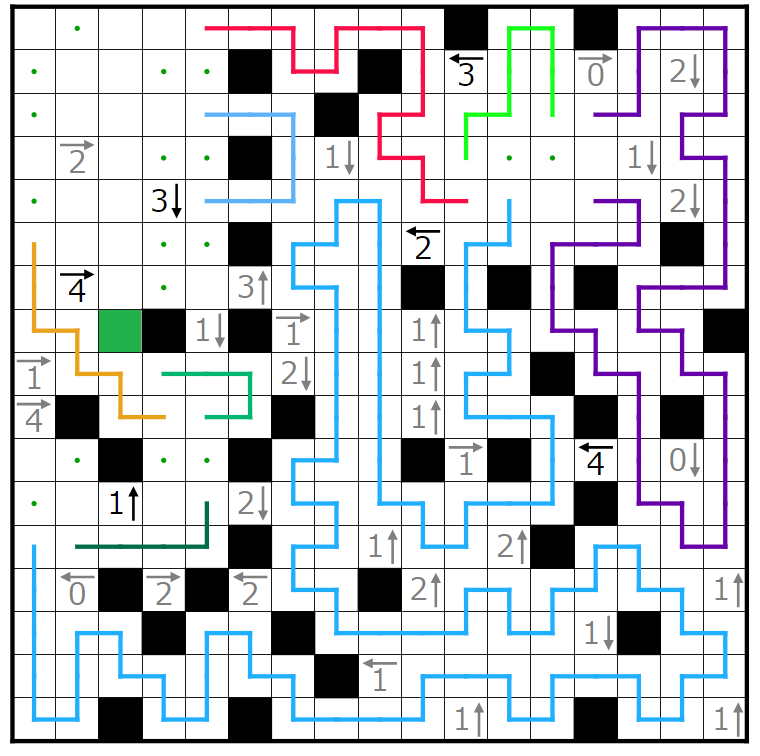
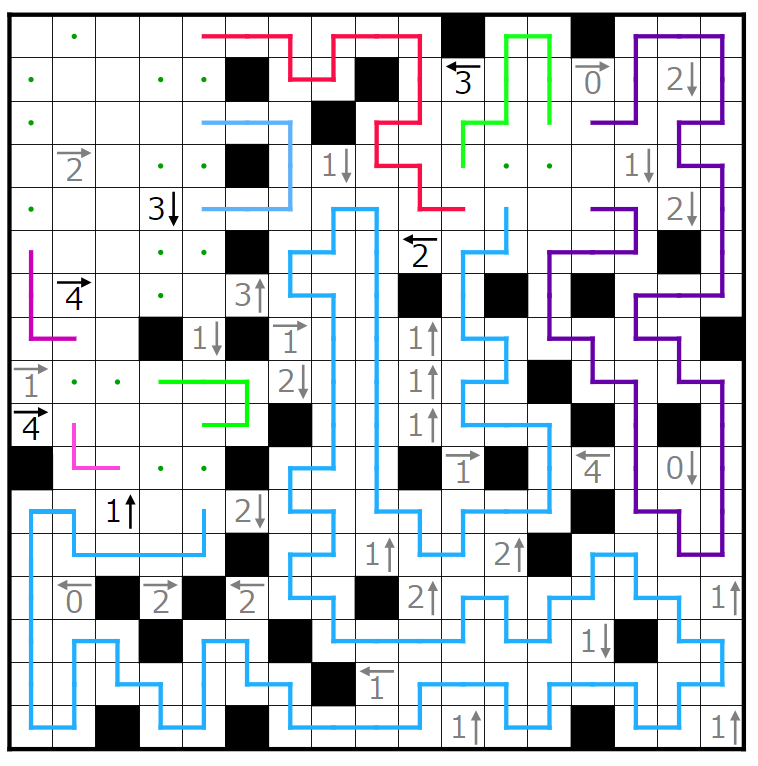
次に、緑で囲んだ4→のヒントに注目します。すでに2個黒マスがあるため赤四角と青四角の部分に計2個黒マスが入ることになります。
今、赤四角に2個黒マスを入れると仮定します。
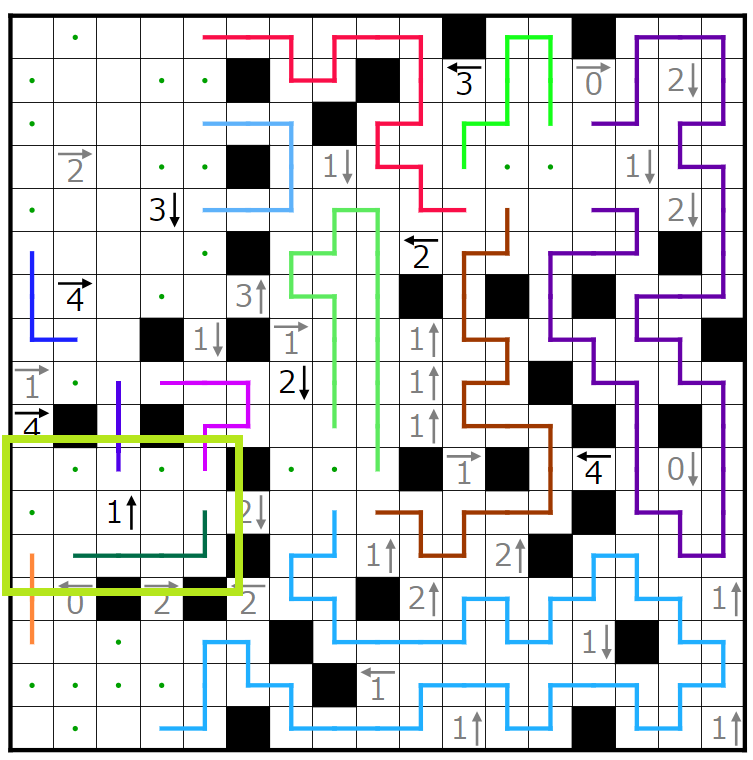
少なくとも囲んだ閉区間に線の端が奇数本であるため矛盾します。

よって赤四角、青四角にはそれぞれ黒マスが1個ずつ入ることが分かり、特に青四角のマスには黒マスが入ることが分かります。
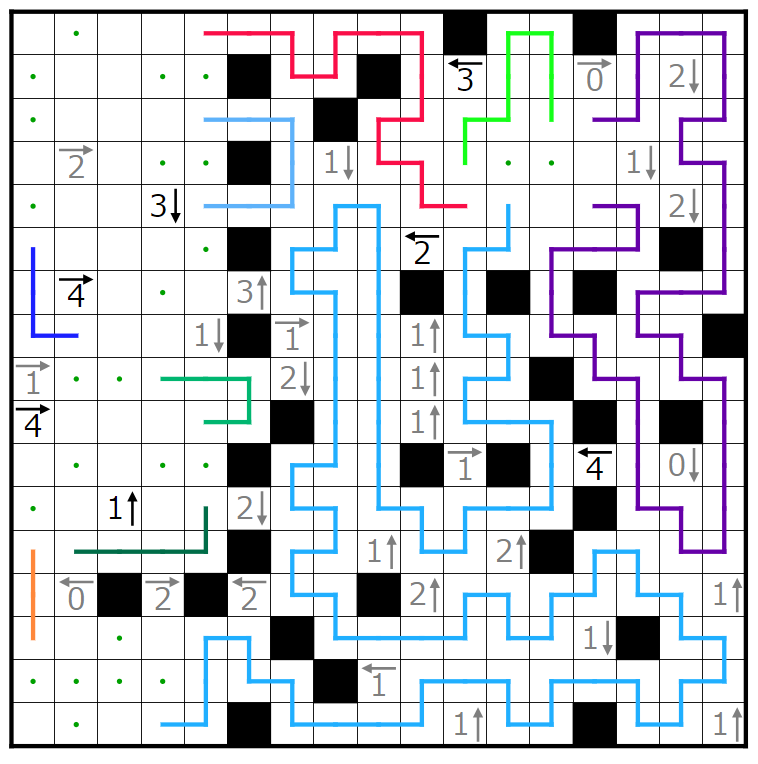
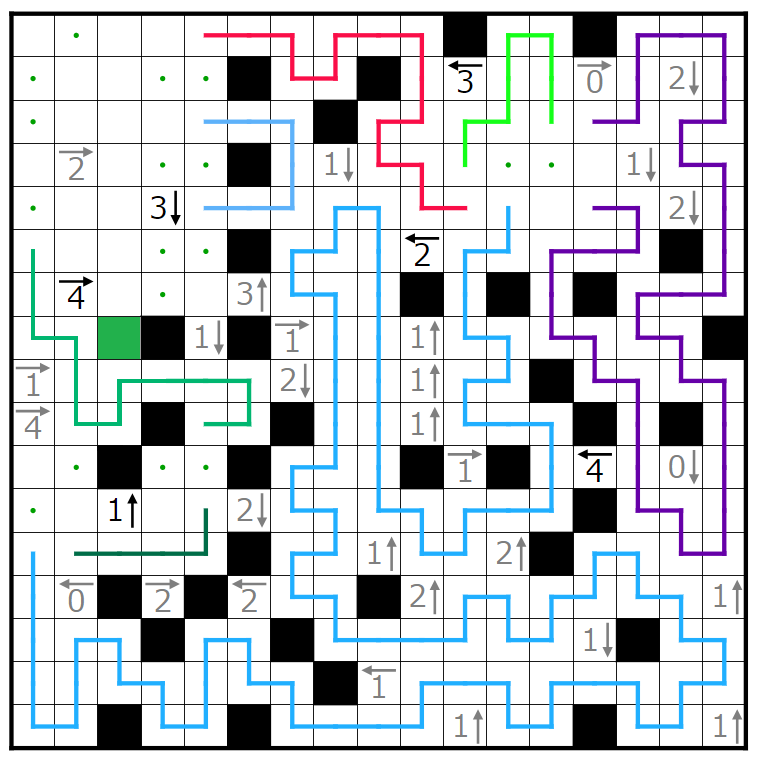
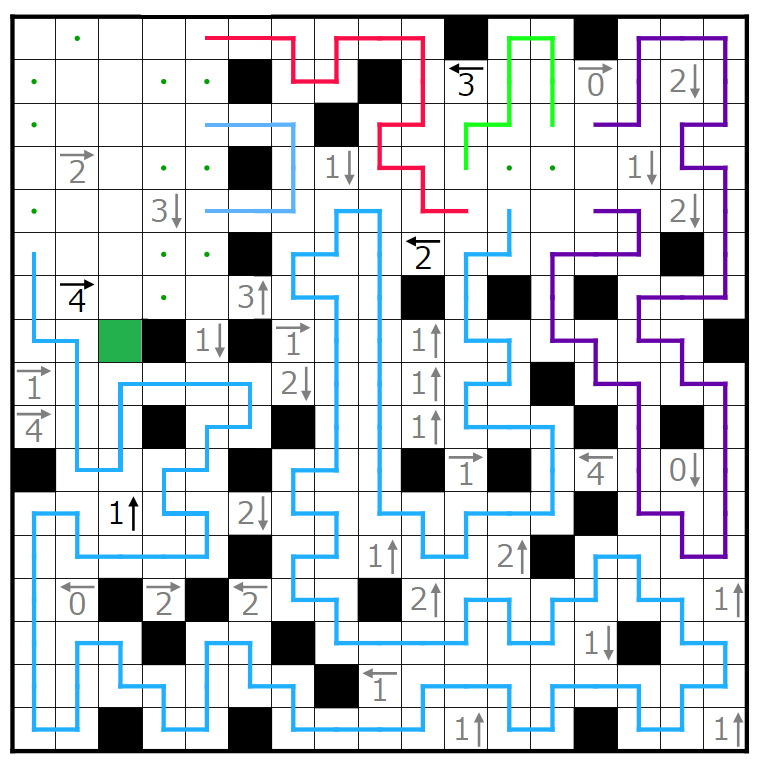
ここまで埋まりました。
さて、終盤です。作っているときは残りの部分が簡単に決まらなければいいやぐらいの気持ちでとりあえず簡単に決まらないパターンを探して採用した感じだったからかややこしい気がします。
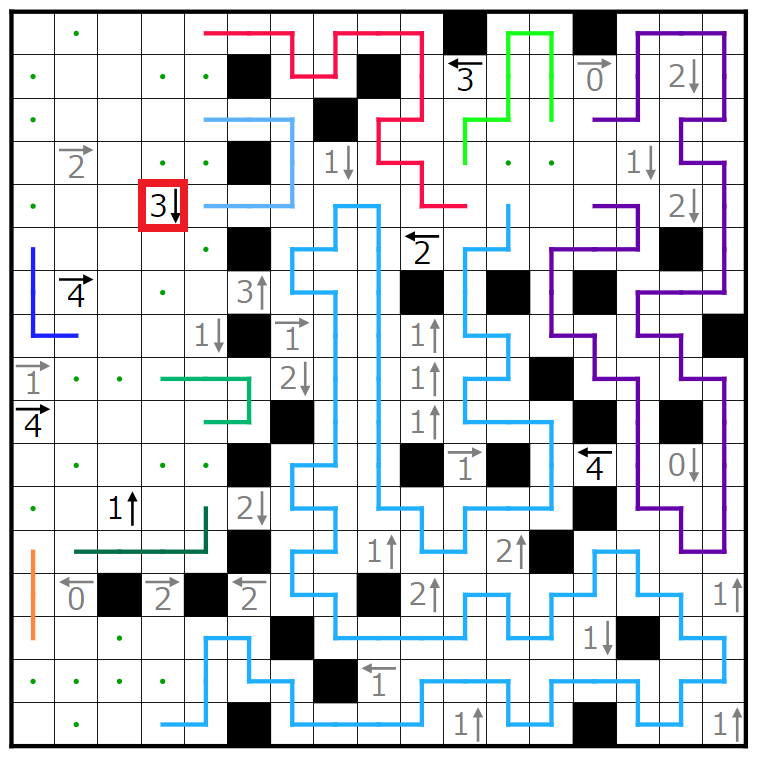
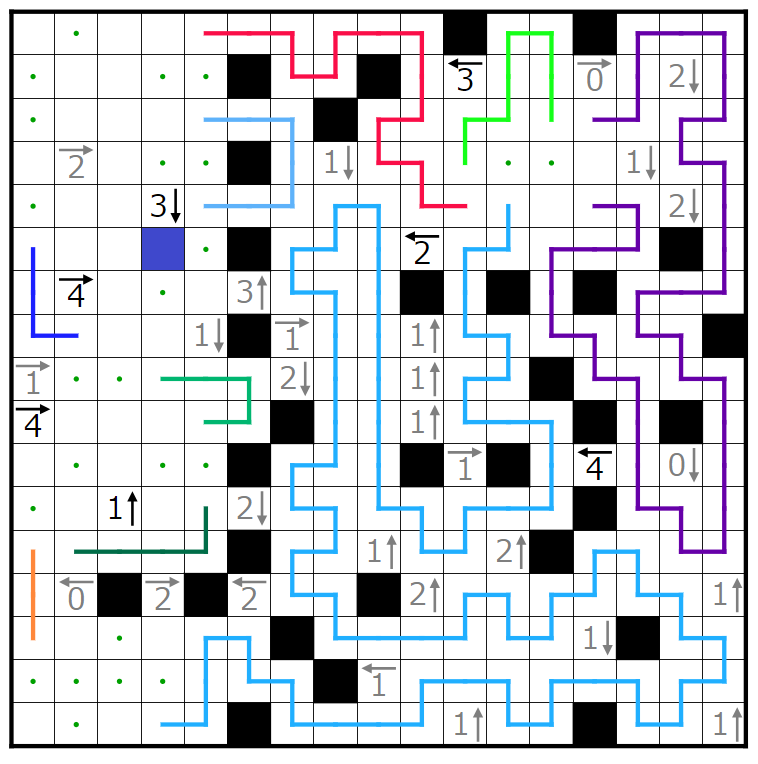
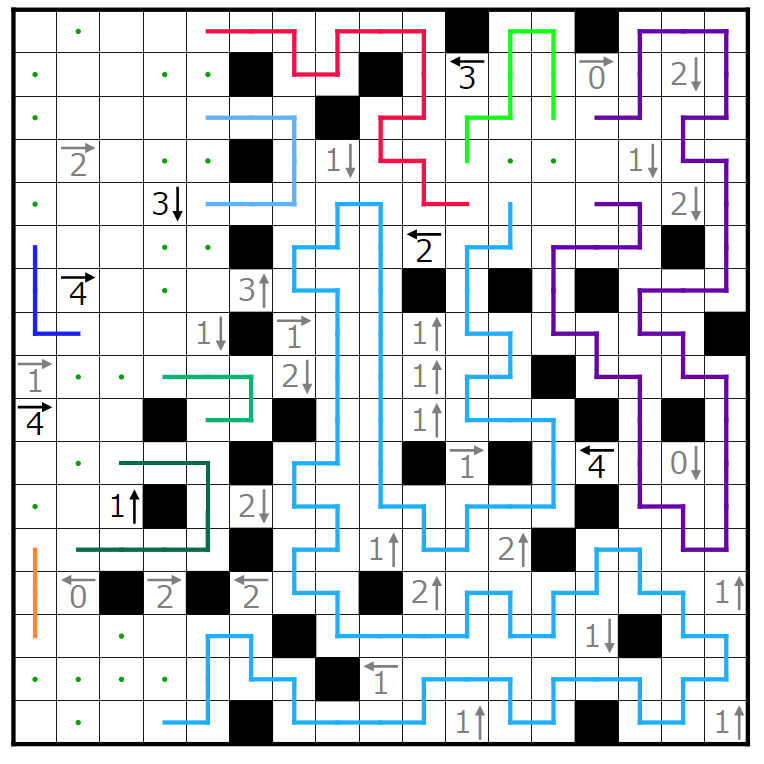
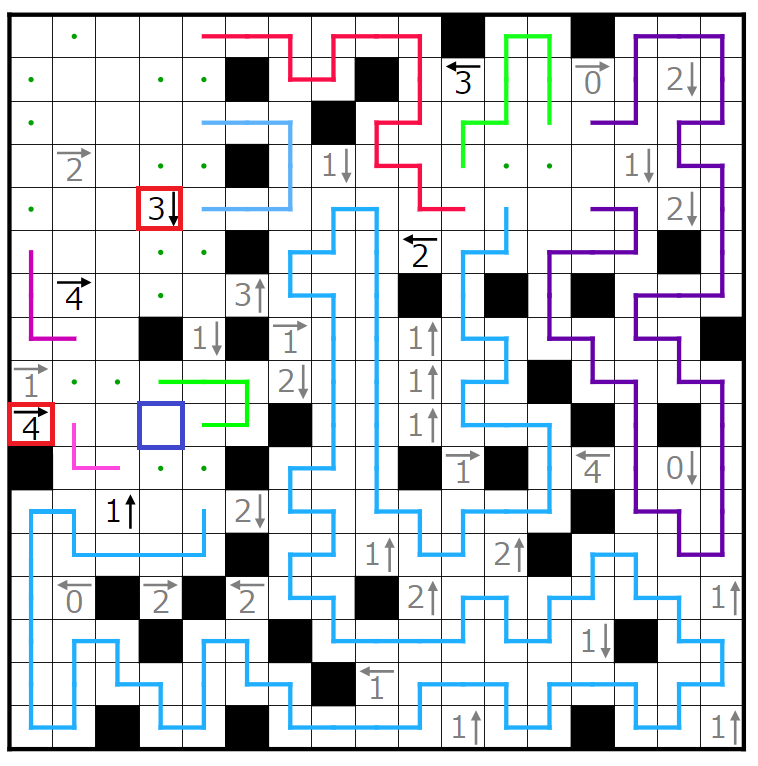
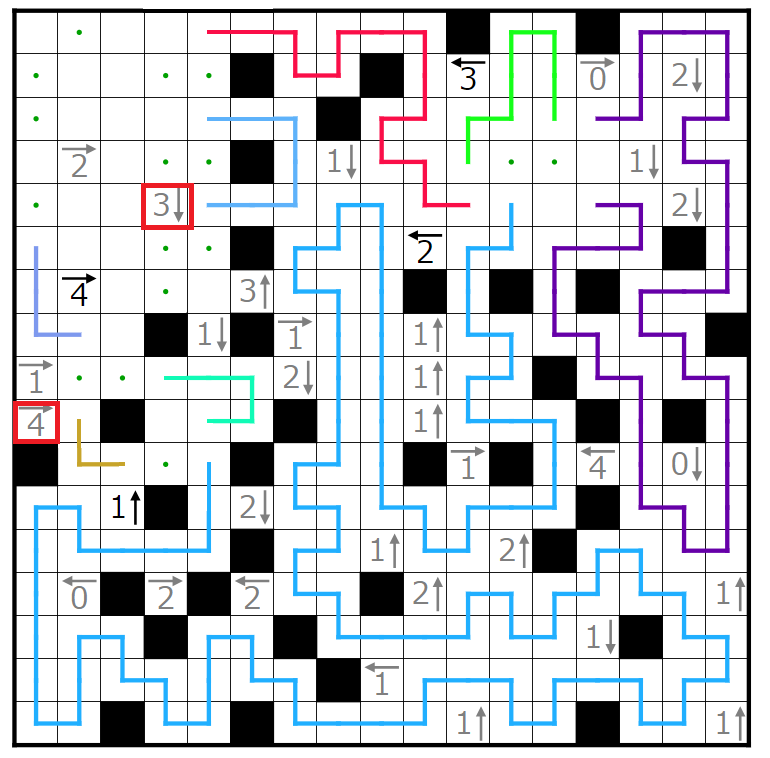
この3↓のヒントに注目します。
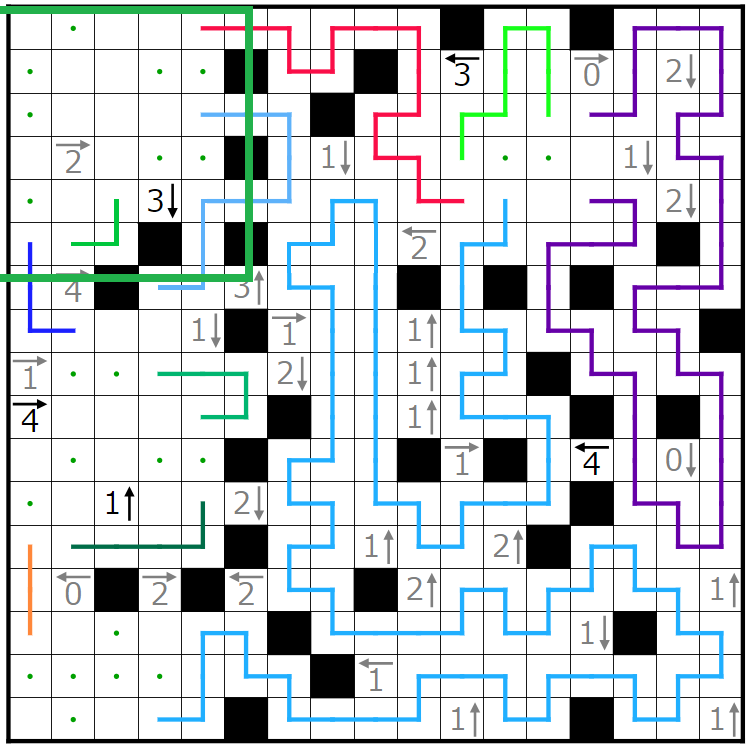
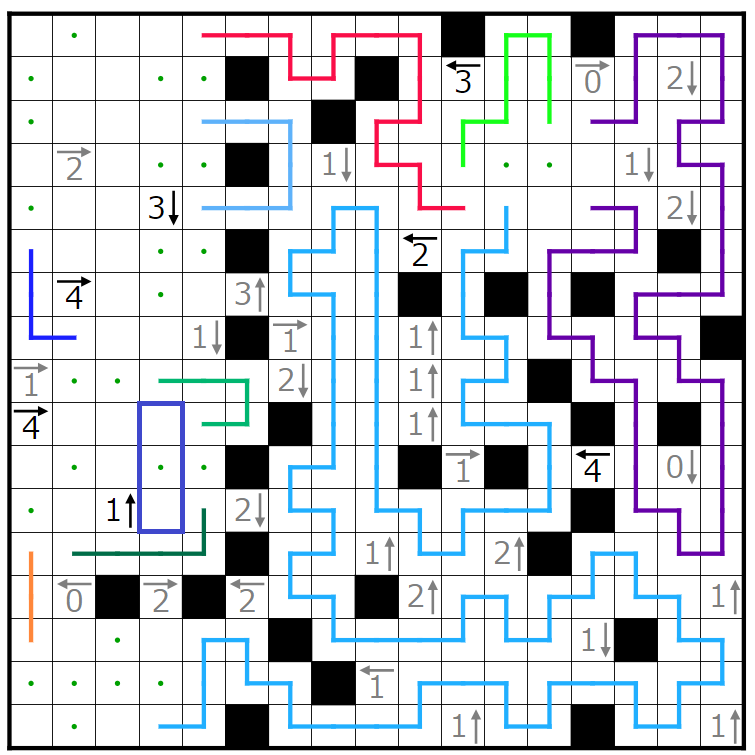


解説は以上になります。長くなりましたが、ここまで読んで頂きありがとうございました!!